题目内容
18.已知函数f(x)=mx2+mx-1.(1)若对于任意x∈R,f(x)<0恒成立,求实数m的取值范围;
(2)若对于任意x∈[0,+∞),f(x)<(m+2)x2恒成立,求实数m的取值范围.
分析 (1)通过m是否为0,利用二次函数的性质转化求解即可.
(2)对于任意x∈[0,+∞),f(x)<(m+2)x2恒成立,列出m的不等式,利用基本不等式求解即可.
解答 解:(1)当m=0时,-1<0,符合对于任意x∈R,f(x)<0恒成立;
当m≠0时,对于任意x∈R,f(x)<0恒成立,即mx2+mx-1<0,可得$\left\{\begin{array}{l}m<0\\△<0\end{array}\right.$,解得-4<m<0,
综上,实数m的取值范围:(-4,0].
(2)对于任意x∈[0,+∞),f(x)<(m+2)x2恒成立,化简得:mx<2x2+1.
当x=0时,不等式恒成立,即m∈R,
当x>0时,$m<2x+\frac{1}{x}$,
因为x>0,所以$2x+\frac{1}{x}≥2\sqrt{2}$,即$m<2\sqrt{2}$,
综上,$m<2\sqrt{2}$.实数m的取值范围:(-∞,$2\sqrt{2}$).
点评 本题考查函数恒成立,二次函数的性质,分类讨论思想的应用,考查计算能力.

练习册系列答案
相关题目
10.已知向量$\overrightarrow a$=(x,1),$\overrightarrow b$=(3,1),若$\overrightarrow a$⊥$\overrightarrow b$,则实数x=( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | -3 | D. | 3 |
7.为了调查高中学生是否喜欢数学与性别的关系,随机抽查男、女学生各 40 名,得到具体数据如表:
(I)根据上面的列联表,能否在犯错误的概率不超过 0.025 的前提下,认为是否喜欢数学与性别有关?
(II)计算这 80 位学生不喜欢数学的频率;(III)用分层抽样的方法从不喜欢数学的男女学生中抽查 6 人进行数学问卷调查,再从中抽取 4 份问卷递交校长办,求至少抽出 3 名女生问卷的概率.
参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
参考数据:
| 是否喜欢数学 | 是 | 否 | 合计 |
| 男生 | 30 | 10 | 40 |
| 女生 | 20 | 20 | 40 |
| 合计 | 50 | 30 | 80 |
(II)计算这 80 位学生不喜欢数学的频率;(III)用分层抽样的方法从不喜欢数学的男女学生中抽查 6 人进行数学问卷调查,再从中抽取 4 份问卷递交校长办,求至少抽出 3 名女生问卷的概率.
参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
参考数据:
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0[来源:] | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
8.已知平面α和两条直线a,b,则下列结论成立的是( )
| A. | 如果a∥α,b∥α,那么a∥b | |
| B. | 如果a∥b,a∥α,b?α,那么b∥α | |
| C. | 如果a∥b,那么α平行于经过b的任何平面 | |
| D. | 如果a∥α,那么a与α内的任何直线平行 |
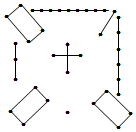 洛书古称龟书,是阴阳五行术数之源,在古代传说中有神龟出于洛水,其甲壳上有如图所示图案,结构是戴九履一,左三右七,二四为肩,六八为足,以五居中,洛书中蕴含的规律奥妙无穷,比如:42+92+22=82+12+62.据此你能得到类似等式是42+32+82=22+72+62.
洛书古称龟书,是阴阳五行术数之源,在古代传说中有神龟出于洛水,其甲壳上有如图所示图案,结构是戴九履一,左三右七,二四为肩,六八为足,以五居中,洛书中蕴含的规律奥妙无穷,比如:42+92+22=82+12+62.据此你能得到类似等式是42+32+82=22+72+62.