题目内容
已知曲线C1=:x2+y2-2 x+2y=0和曲线C2:
x+2y=0和曲线C2: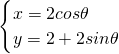 (θ为参数)关于直线l1.对称,直线l2过点(
(θ为参数)关于直线l1.对称,直线l2过点( ,-1)且与l1的夹角为60°,则直线l2的方程为
,-1)且与l1的夹角为60°,则直线l2的方程为
- A.y=
 x-4
x-4 - B.x=
 或y=-
或y=-
- C.y=-

- D.x=
 或y=
或y= x-4
x-4
B
分析:利用两圆的方程相减,求出两等圆的对称轴直线l1的方程,再设所求直线的斜率为k,代入两条直线的夹角公式求出夹角的正确的值,列出关于k的方程即可得到k的值.
解答:曲线C2: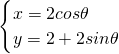 (θ为参数)化为直角坐标方程为x2+(y-2)2=4,又曲线C1:x2+y2-2
(θ为参数)化为直角坐标方程为x2+(y-2)2=4,又曲线C1:x2+y2-2 x+2y=0,k2
x+2y=0,k2
两方程相减得直线l1:x- y=0.
y=0.
设直线l1,l2的斜率分别为 k1,k2,l1与l2的夹角为θ=60°,
则k1= .
.
则tan60°= =
= ,解得k2=0
,解得k2=0
另外,当直线l2的斜率不存在时,即l2的方程为:x= 也符合要求,
也符合要求,
则直线l2的方程为:x= 或y=-
或y=-
故选B.
点评:本题考查直线方程求解,两条直线的夹角公式的应用.求直线方程时,若从斜率角度求解,务必注意斜率不存在情形,否则容易漏解.
分析:利用两圆的方程相减,求出两等圆的对称轴直线l1的方程,再设所求直线的斜率为k,代入两条直线的夹角公式求出夹角的正确的值,列出关于k的方程即可得到k的值.
解答:曲线C2:
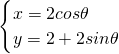 (θ为参数)化为直角坐标方程为x2+(y-2)2=4,又曲线C1:x2+y2-2
(θ为参数)化为直角坐标方程为x2+(y-2)2=4,又曲线C1:x2+y2-2 x+2y=0,k2
x+2y=0,k2两方程相减得直线l1:x-
 y=0.
y=0.设直线l1,l2的斜率分别为 k1,k2,l1与l2的夹角为θ=60°,
则k1=
 .
.则tan60°=
 =
= ,解得k2=0
,解得k2=0另外,当直线l2的斜率不存在时,即l2的方程为:x=
 也符合要求,
也符合要求,则直线l2的方程为:x=
 或y=-
或y=-
故选B.
点评:本题考查直线方程求解,两条直线的夹角公式的应用.求直线方程时,若从斜率角度求解,务必注意斜率不存在情形,否则容易漏解.

练习册系列答案
相关题目
已知曲线C1:x2+y2-2x=0和曲线C2:y=xcosθ-sinθ(θ为锐角),则C1与C2的位置关系为( )
| A、相离 | B、相切 | C、相交 | D、以上情况均有可能 |
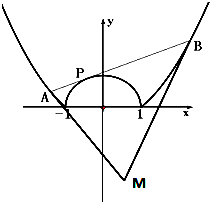 如图,已知曲线C1:x2+y2=1(|x|<1),C2:x2=8y+1(|x|≥1),动直线l与C1相切,与C2相交于A,B两点,曲线C2在A,B处的切线相交于点M.
如图,已知曲线C1:x2+y2=1(|x|<1),C2:x2=8y+1(|x|≥1),动直线l与C1相切,与C2相交于A,B两点,曲线C2在A,B处的切线相交于点M.