题目内容
已知曲线C1：x2+y2+2kx+（4k+10）y+10k+20=0 （k≠-1），当k取不同值时，曲线C表示不同的圆，且这些圆的圆心共线，则这条直线的方程是分析：先把曲线方程整理成圆的标准方程，设出圆心的坐标，进而根据曲线的方程用k表示出圆心的横坐标和纵坐标，联立方程求得x和y的关系式．
解答：解：整理曲线方程得（x+k）2+（y+2k+5）2=k2+（2k+5）2，
设圆的圆心为（x，y）
则
求得y=2x-5，即2x-y-5=0
故答案为：2x-y-5=0
设圆的圆心为（x，y）
则
|
故答案为：2x-y-5=0
点评：本题主要考查了直线圆的位置关系，圆的标准方程，点的轨迹方程等．考查了学生综合分析问题和解决问题的能力．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
已知曲线C1：x2+y2-2x=0和曲线C2：y=xcosθ-sinθ（θ为锐角），则C1与C2的位置关系为（ ）
| A、相离 | B、相切 | C、相交 | D、以上情况均有可能 |
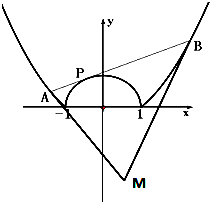如图，已知曲线C1：x2+y2=1（|x|＜1），C2：x2=8y+1（|x|≥1），动直线l与C1相切，与C2相交于A，B两点，曲线C2在A，B处的切线相交于点M．