Question

16．函数f（x）=x³-$\frac{ln|x|}{x}$的图象大致为（　　）

• A．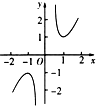
• B．
• C．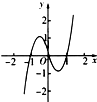
• D．

Answer 1

分析 判断函数的奇偶性，利用特殊值求解点的坐标，判断即可．

解答 解：函数f（x）=x³-$\frac{ln|x|}{x}$，满足f（-x）=-x³+$\frac{ln|x|}{x}$=-（x³-$\frac{ln|x|}{x}$）=-f（x）．
即：f（-x）=-f（x），函数是奇函数，
x=1时，f（1）=1．
观察选项可知：A满足题意．
故选：A．

点评 本题考查函数的图象的判断，利用函数的奇偶性以及函数经过的特殊点，是解题的关键．