题目内容
已知cosα=
,cos(α+β)=-
,且α∈(0,
),α+β∈(
,π),则cosβ的值为 .
| 1 |
| 7 |
| 11 |
| 14 |
| π |
| 2 |
| π |
| 2 |
考点:两角和与差的余弦函数
专题:三角函数的求值
分析:由题意分别可得sinα和sin(α+β)的值,而cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα,代入计算可得.
解答:
解:∵cosα=
且α∈(0,
),
∴sinα=
=
,
又∵cos(α+β)=-
且α+β∈(
,π),
∴sin(α+β)=
=
,
∴cosβ=cos[(α+β)-α]
=cos(α+β)cosα+sin(α+β)sinα
=-
×
+
×
=
故答案为:
| 1 |
| 7 |
| π |
| 2 |
∴sinα=
| 1-cos2α |
4
| ||
| 7 |
又∵cos(α+β)=-
| 11 |
| 14 |
| π |
| 2 |
∴sin(α+β)=
| 1-cos2(α+β) |
5
| ||
| 14 |
∴cosβ=cos[(α+β)-α]
=cos(α+β)cosα+sin(α+β)sinα
=-
| 11 |
| 14 |
| 1 |
| 7 |
5
| ||
| 14 |
4
| ||
| 7 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查两角和与差的三角函数公式,整体法是解决问题的关键,属中档题.

练习册系列答案
相关题目
已知函数f(x)=(sinx+cosx)2+2cos2x.
(Ⅰ)求函数f(x)图象的对称轴方程;
(Ⅱ)设△ABC的三个角A,B,C所对的边分别是a,b,c,且f(B)=3,b=3,求a•c的取值范围.
(Ⅰ)求函数f(x)图象的对称轴方程;
(Ⅱ)设△ABC的三个角A,B,C所对的边分别是a,b,c,且f(B)=3,b=3,求a•c的取值范围.
如果实数x、y满足条件
,那么z=-2x+y的最大值为( )
|
| A、1 | B、2 | C、3 | D、4 |
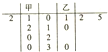 2014年1月8日是传统的腊八节,大家开始购买年货,某淘宝网店趁势推出“抢红包”的促销活动,已知每人有5次抢红包的机会,每次可得1至30元不等的红包,甲、乙二人在这5次抢红包活动中获得红包金额的茎叶图如图所示,若甲5次获得红包金额的均值为
2014年1月8日是传统的腊八节,大家开始购买年货,某淘宝网店趁势推出“抢红包”的促销活动,已知每人有5次抢红包的机会,每次可得1至30元不等的红包,甲、乙二人在这5次抢红包活动中获得红包金额的茎叶图如图所示,若甲5次获得红包金额的均值为