题目内容
【题目】已知函数f(x)=x2+(x2-3x)lnx
(1)求函数f(x)在x=e处的切线方程
(2)对任意的x![]() )都存在正实数a,使得方程f(x)=a至少有2个实根, 求a的最小值
)都存在正实数a,使得方程f(x)=a至少有2个实根, 求a的最小值
【答案】(1)(5e-6)x-y-3e2+3e=0(2)1
【解析】分析:(1)求出![]() ,由
,由![]() 的值可得切点坐标,由
的值可得切点坐标,由![]() 的值,可得切线斜率,利用点斜式可得曲线
的值,可得切线斜率,利用点斜式可得曲线![]() 在点
在点![]() 处的切线方程;(2)首先可得
处的切线方程;(2)首先可得![]() 是方程的根,只需方程另外至少一个根即可,利用导数研究函数的单调性,结合函数图象,可得函数的极值与最值,从而可得
是方程的根,只需方程另外至少一个根即可,利用导数研究函数的单调性,结合函数图象,可得函数的极值与最值,从而可得![]() 的最大值.
的最大值.
详解:(1)f/(x)=3x-3+(2x-3)lnx ![]() k=f/(e)=5e-6切点为:(e,2
k=f/(e)=5e-6切点为:(e,2![]() -3e)
-3e)
切线方程为: y-2![]() +3e=(5e-6)(x-e) (5e-6)x-y-3
+3e=(5e-6)(x-e) (5e-6)x-y-3![]() +3e=0
+3e=0
(2)令f/(x)=0 即3x-3+(2x-3)lnx=0 显然x=1是方程的根
而f//(x)=2lnx![]() 易知f//(x)在(0,
易知f//(x)在(0,![]() )上递增,容易验证f//(
)上递增,容易验证f//(![]() )=3-3e
)=3-3e![]() f//(1)
f//(1)![]() ,
,![]() 存在x1
存在x1![]() 使得f//(x1)=0
使得f//(x1)=0
所以当x![]() 1)时,f//(x)
1)时,f//(x)![]() ,
,![]() f/(x)递减,
f/(x)递减,
当x![]() 1,
1,![]() 时,f//(x)
时,f//(x)![]() ,
,![]() f/(x)递增
f/(x)递增
且f/(x1)![]() /(1)=0,又f(
/(1)=0,又f(![]() )=
)=![]() ,故存在x2
,故存在x2![]() x1)使得f/(x2) =0,列出下表:
x1)使得f/(x2) =0,列出下表:
x | (0,x2) | x2 | (x2,1) | 1 | (1, |
f/(x) | + | 0 | - | 0 | + |
f(x) | 增 | 极大值 | 减 | 极小值 | 增 |
所以f(x)在x=x2处取极大值;在![]() 处取得极小值.因f(1)=1;x
处取得极小值.因f(1)=1;x![]() 0时f(x)
0时f(x)![]()
作出f(x)的示意图可知: a的最小值为1

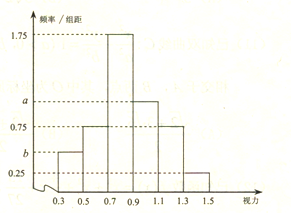
【题目】某品牌汽车的![]() 店,对最近100份分期付款购车情况进行统计,统计情况如下表所示.已知分9期付款的频率为0.4;该店经销一辆该品牌汽车,若顾客分3期付款,其利润为1万元;分6期或9期付款,其利润为2万元;分12期付款,其利润为3万元.
店,对最近100份分期付款购车情况进行统计,统计情况如下表所示.已知分9期付款的频率为0.4;该店经销一辆该品牌汽车,若顾客分3期付款,其利润为1万元;分6期或9期付款,其利润为2万元;分12期付款,其利润为3万元.
付款方式 | 分3期 | 分6期 | 分9期 | 分12期 |
频数 | 20 | 20 |
|
|
(1)若以上表计算出的频率近似替代概率,从该店采用分期付款购车的顾客(数量较大)中随机抽取3为顾客,求事件![]() :“至多有1位采用分6期付款“的概率
:“至多有1位采用分6期付款“的概率![]() ;
;
(2)按分层抽样方式从这100为顾客中抽取5人,再从抽取的5人中随机抽取3人,记该店在这3人身上赚取的总利润为随机变量![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.