题目内容
10.已知定义在R上的函数y=f(x)满足下列三个条件:①对任意的x∈R都有f(x+2)=-f(x);
②对于任意的0≤x1<x2≤2,都有f(x1)<f(x2),
③y=f(x+2)的图象关于y轴对称,
则下列结论中正确的是( )
| A. | f(4.5)<f(6.5)<f(7) | B. | f(7)<f(6.5)<f(4.5) | C. | f(7)<f(4.5)<f(6.5) | D. | f(4.5)<f(7)<f(6.5) |
分析 对任意的x∈R都有f(x+2)=-f(x),得到函数是一个周期函数T=4,对于任意的0≤x1<x2≤2,都有f(x1)<f(x2),得到函数在[0,2]上是一个递增函数,根据f(x+2)的图象关于y轴对称,得到f(x)的图象关于x=2对称.
解答 解:∵对任意的x∈R都有f(x+2)=-f(x),
∴函数是一个周期函数T=4,
∵对于任意的0≤x1<x2≤2,都有f(x1)<f(x2),
∴函数在[0,2]上是一个递增函数,
且f(0)=-f(2),f(1)=0,
∵f(x+2)的图象关于y轴对称,
∴f(x)的图象关于x=2对称,
f(4.5)=f(0.5)<0,
f(6.5)=f(2.5)>0,
f(7)=f(3)=f(-1)=-f(1)=0,
∵函数在[0,2]上是一个递增函数,
∴f(4.5)<f(7)<f(6.5)
故选:D.
点评 本题考查函数的周期性和函数的单调性,是一个关于函数性质的综合题目,解题的关键是把几个函数的自变量通过变化,放到同一个单调区间上.

练习册系列答案
相关题目
15.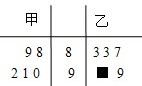 如图的茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率为( )
如图的茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率为( )
 如图的茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率为( )
如图的茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率为( )| A. | $\frac{3}{10}$ | B. | $\frac{7}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |