题目内容
1.已知f(x)=xlnx.(1)求曲线f(x)在x=e处的切线方程.
(2)求函数f(x)的单调区间.
分析 (1)求出函数的导数,求出切线的斜率,切点坐标,然后求解切线方程.
(2)利用导函数的符号,判断函数的单调性,求解函数的单调区间即可.
解答 解:(1)由f(x)=xln x得f′(x)=ln x+1(x>0),
所以切线斜率为f′(x)=lne+1=2
切点坐标为(e,e),
所以切线方程为y-e=2(x-e)即y=2x-e;
(2)f′(x)=ln x+1(x>0),
令f′(x)=0,得x=$\frac{1}{e}$.
∴当x∈$(0,\frac{1}{e})$时,f′(x)<0;
当x∈$(\frac{1}{e},+∞)$时,f′(x)>0,
∴f(x)=xln x在$(0,\frac{1}{e})$单调递减,在$(\frac{1}{e},+∞)$单调递增.
点评 本题考查函数的导数的综合应用,切线方程的求法,函数的单调性的判断,考查计算能力.

练习册系列答案
相关题目
16.已知$|{\overrightarrow a}|=1$,$|{\overrightarrow b}|=\sqrt{2}$,且$\overrightarrow a⊥(\overrightarrow a+\overrightarrow b)$,则向量$\overrightarrow a$与向量$\overrightarrow b$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{3π}{4}$ | D. | $\frac{π}{4}$或$\frac{3π}{4}$ |
13.$|{\frac{1-2i}{2+i}}|$=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | -i | D. | 2 |
11.若函数f(x)=lnx与函数g(x)=x2+2x+a(x<0)有公切线,则实数a的取值范围为( )
| A. | (ln$\frac{1}{2e}$,+∞) | B. | (-1,+∞) | C. | (1,+∞) | D. | (-ln2,+∞) |
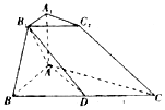 如图所示的三棱台ABC-A1B1C1中,AA1⊥平面ABC,AB⊥BC,AA1=1,AB=2,BC=4,∠ABB1=45°.
如图所示的三棱台ABC-A1B1C1中,AA1⊥平面ABC,AB⊥BC,AA1=1,AB=2,BC=4,∠ABB1=45°.