题目内容

2．已知数列{sinan}是公比为-1的等比数列，若数列{an}是等差数列，则其公差可能是（　　）
A．-$\frac{3π}{2}$B．-$\frac{π}{2}$C．πD．2π

分析 由等比数列和等差数列的性质，结合已知条件推导出sin（an+d）=-sinan，由此能求出公差d可能是π．

解答 解：∵数列{sinan}是公比为-1的等比数列，
∴$\frac{sin{a}_{n+1}}{sin{a}_{n}}$=-1，
∵数列{an}是等差数列，
∴$\frac{sin（{a}_{n}+d）}{sin{a}_{n}}$=-1，
∴sin（an+d）=-sinan，
∴公差d可能是π．
故选：C．

点评 本题考查等差数列的一个公差的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．

练习册系列答案
相关题目
12．已知a，b，c分别为△ABC的三个内角A，B，C的对边，a=2且（2+b）（sinA-sinB）=（c-b）sinC
（1）求角A的大小；
（2）求△ABC的面积的最大值．
13．设实数a，b满足0≤a，b≤8，且b2=16+a2，则b-a的最大值为4．
10．已知函数y=msinx+3cosx（m∈R）的图象与直线y=n（n为常数）相邻两个交点的横坐标为x1=$\frac{π}{12}$，x2=$\frac{7π}{12}$，则m的值为3$\sqrt{3}$，n的值为3$\sqrt{2}$．
17．设椭圆C的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0），过M（-b，0）的直线l与椭圆C交于A，B两点
（1）已知椭圆C的离心率为$\frac{\sqrt{3}}{3}$，过N（b，0）作x轴的垂线与直线l交于P．且NP的中点在C上．求直线1的倾斜角；
（2）设B关于坐标原点的对称点为Q，求△ABQ的面积最大值（用a，b表示）．
7．在△ABC中，a，b，c分别是角A，B，C的对边，若C=30°，b=3，△ABC的面积为$\frac{3\sqrt{3}}{4}$，则c=（　　）
A．1B．2C．$\frac{\sqrt{3}}{2}$D．$\sqrt{3}$
14．运行如图程序框图，则当输出y的值最大时，输入的x值等于（　　）
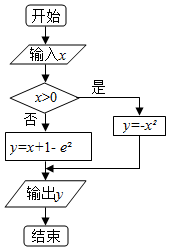
A．0B．1C．-1D．2
11．$\int_0^1{|x-1|}dx$=（　　）
A．1B．2C．3D．$\frac{1}{2}$
12．已知函数f（x）=$\frac{mx}{lnx}$，曲线y=f（x）在点（e2，f（e2））处的切线与直线2x+y=0垂直（其中e为自然对数的底数）．
（Ⅰ）求f（x）的解析式及单调减区间；
（Ⅱ）若函数g（x）=f（x）-$\frac{k{x}^{2}}{x-1}$无零点，求k的取值范围．．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网