题目内容
已知函数f(x)=cos x(sin x+cos x)- .
.
(1)若0<α< ,且sin α=
,且sin α= ,求f(α)的值;
,求f(α)的值;
(2)求函数f(x)的最小正周期及单调递增区间.
解:法一 (1)因为0<α< ,sin α=
,sin α= ,
,
所以cos α= .
.
所以f(α)= (
( +
+ )-
)- =
= .
.
(2)因为f(x)=sin xcos x+cos2x-
= sin 2x+
sin 2x+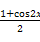 -
-
= sin 2x+
sin 2x+ cos 2x
cos 2x
= sin(2x+
sin(2x+ ),
),
所以T=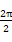 =π.
=π.
由2kπ- ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,k∈Z,
,k∈Z,
得kπ-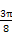 ≤x≤kπ+
≤x≤kπ+ ,k∈Z.
,k∈Z.
所以f(x)的单调递增区间为[kπ-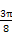 ,kπ+
,kπ+ ],k∈Z.
],k∈Z.
法二 f(x)=sin xcos x+cos2x-
= sin 2x+
sin 2x+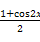 -
-
= sin 2x+
sin 2x+ cos 2x
cos 2x
= sin(2x+
sin(2x+ ).
).
(1)因为0<α< ,sin α=
,sin α= ,
,
所以α= ,
,
从而f(α)= sin(2α+
sin(2α+ )=
)= sin
sin 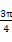 =
= .
.
(2)T=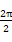 =π.
=π.
由2kπ- ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,k∈Z,
,k∈Z,
得kπ-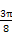 ≤x≤kπ+
≤x≤kπ+ ,k∈Z.
,k∈Z.
所以f(x)的单调递增区间为[kπ-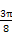 ,kπ+
,kπ+ ],k∈Z.
],k∈Z.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 +
+ +
+ 的值.
的值. ,
,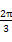 )=-f(
)=-f( 个单位长度
个单位长度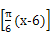 (x=1,2,3,…,12)来表示,已知6月份的平均气温最高,为28 ℃,12月份的平均气温最低,为18 ℃,则10月份的平均气温值为 ℃.
(x=1,2,3,…,12)来表示,已知6月份的平均气温最高,为28 ℃,12月份的平均气温最低,为18 ℃,则10月份的平均气温值为 ℃.  ,cos(α+β)=-
,cos(α+β)=- ,α∈(0,
,α∈(0, ),α+β∈(
),α+β∈(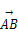 =3a,则点B的坐标为( )
=3a,则点B的坐标为( )