题目内容
如图,过圆O外一点M作它的一条切线,切点为A,过A点作直线AP垂直直线OM,垂足为P。
(Ⅰ)证明:![]()
(Ⅱ)N为线段AP上一点,直线NB垂直直线ON,且交圆O于B点,过B点的切线交直线ON于K。证明:![]()

证明:(Ⅰ)因为MA是圆O的切线,所以OA⊥AM
又因为AP⊥OM,在Rt△OAM中,由射影定理知,
OA2=OM?OP。
(Ⅱ)因为BK是圆O的切线,BN⊥OK,
同(Ⅰ),有OB2=ON?OK,又OB=OA,
所以OP?OM=ON?OK,即![]() ,
,
又∠NOP=∠MOK,
所以△ONP∽△OMK,故∠OKM=∠OPN=90º。

练习册系列答案
相关题目
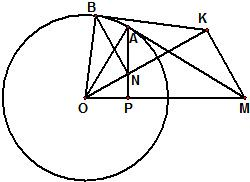 如图,过圆O外一点M作它的一条切线,切点为A,过A作直线AP垂直直线OM,垂足为P.
如图,过圆O外一点M作它的一条切线,切点为A,过A作直线AP垂直直线OM,垂足为P.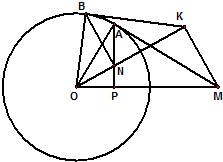
 (2012•洛阳一模)如图,过圆O外一点M作它的一条切线,切点为A,过A作直线AP垂直于直线OM,垂足为P,N为线段AP上一点,直线NB垂直于直线ON,且交圆O于B点.在B点处的切线交直线ON于K.
(2012•洛阳一模)如图,过圆O外一点M作它的一条切线,切点为A,过A作直线AP垂直于直线OM,垂足为P,N为线段AP上一点,直线NB垂直于直线ON,且交圆O于B点.在B点处的切线交直线ON于K.
 ;
;