题目内容
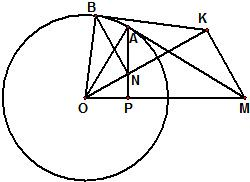 如图,过圆O外一点M作它的一条切线,切点为A,过A作直线AP垂直直线OM,垂足为P.
如图,过圆O外一点M作它的一条切线,切点为A,过A作直线AP垂直直线OM,垂足为P.(1)证明:OM•OP=OA2;
(2)N为线段AP上一点,直线NB垂直直线ON,且交圆O于B点.过B点的切线交直线ON于K.证明:∠OKM=90°.
分析:(1)在三角形OAM中考虑,因为MA是圆O的切线,所以OA⊥AM,从而由射影定理即得;
(2)结合(1)问的结论,利用比例线段证明两个三角形△ONP、△OMK相似,通过对应角相等即可得.
(2)结合(1)问的结论,利用比例线段证明两个三角形△ONP、△OMK相似,通过对应角相等即可得.
解答:证明:(1)因为MA是圆O的切线,
所以OA⊥AM,又因为AP⊥OM,
在Rt△OAM中,由射影定理知OA2=OM•OP,
故OM•OP=OA2得证.
(2)因为BK是圆O的切线,BN⊥OK,同(1)有:
OB2=ON•OK,又OB=OA,
所以OM•OP=ON•OK,即
=
,又∠NOP=∠MOK,
所以△ONP~△OMK,
故∠OKM=∠OPN=90°.
即有:∠OKM=90°.
所以OA⊥AM,又因为AP⊥OM,
在Rt△OAM中,由射影定理知OA2=OM•OP,
故OM•OP=OA2得证.
(2)因为BK是圆O的切线,BN⊥OK,同(1)有:
OB2=ON•OK,又OB=OA,
所以OM•OP=ON•OK,即
| ON |
| OP |
| OM |
| OK |
所以△ONP~△OMK,
故∠OKM=∠OPN=90°.
即有:∠OKM=90°.
点评:本题考查的高考考点是圆的有关知识及应用、切割线定理的运用,易错点:对有关知识掌握不到位而出错,高考对平面几何的考查一直要求不高,故要重点掌握,它是我们的得分点之一.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
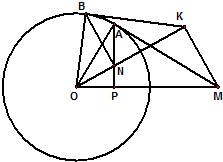
 (2012•洛阳一模)如图,过圆O外一点M作它的一条切线,切点为A,过A作直线AP垂直于直线OM,垂足为P,N为线段AP上一点,直线NB垂直于直线ON,且交圆O于B点.在B点处的切线交直线ON于K.
(2012•洛阳一模)如图,过圆O外一点M作它的一条切线,切点为A,过A作直线AP垂直于直线OM,垂足为P,N为线段AP上一点,直线NB垂直于直线ON,且交圆O于B点.在B点处的切线交直线ON于K.
 ;
;