题目内容
如图,过圆O外一点M作它的一条切线,切点为A,过A作直线AP垂直直线OM,垂足为P;N为线段AP上一点,直线NB垂直直线ON,且交圆O于B点;过B点的切线交直线ON于K,则∠OKM=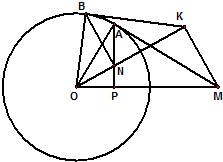
分析:首先根据题中圆的切线条件再依据切割线定理求得一个线段的比例式,再根据相似三角形的判定方法可求得△ONP和△OMK相似,由相似得对应角相等即可.
解答:解:因为BK是圆O的切线,BN⊥OK.
有OB2=ON•OK,又OB=OA,
所以OP•OM=ON•OK,
即
=
.
又∠NOP=∠MOK,
所以△ONP∽△OMK,故∠OKM=∠OPN=90°.
故填:90°.
有OB2=ON•OK,又OB=OA,
所以OP•OM=ON•OK,
即
| ON |
| OP |
| OM |
| OK |
又∠NOP=∠MOK,
所以△ONP∽△OMK,故∠OKM=∠OPN=90°.
故填:90°.
点评:此题综合运用了切割线定理、切线的性质定理以及与圆有关的相似三角形,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
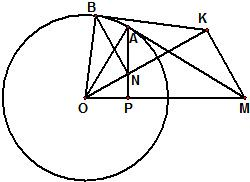 如图,过圆O外一点M作它的一条切线,切点为A,过A作直线AP垂直直线OM,垂足为P.
如图,过圆O外一点M作它的一条切线,切点为A,过A作直线AP垂直直线OM,垂足为P. (2012•洛阳一模)如图,过圆O外一点M作它的一条切线,切点为A,过A作直线AP垂直于直线OM,垂足为P,N为线段AP上一点,直线NB垂直于直线ON,且交圆O于B点.在B点处的切线交直线ON于K.
(2012•洛阳一模)如图,过圆O外一点M作它的一条切线,切点为A,过A作直线AP垂直于直线OM,垂足为P,N为线段AP上一点,直线NB垂直于直线ON,且交圆O于B点.在B点处的切线交直线ON于K.
 ;
;