题目内容
设向量 =(cos2x,1),
=(cos2x,1), =(1,
=(1, sin2x),x∈R,函数f(x)=
sin2x),x∈R,函数f(x)= •
• .
.
(I )求函数f(x)的最小正周期及对称轴方程;
(II)当x∈[0, ]时,求函数f(x)的值域.
]时,求函数f(x)的值域.
解:(Ⅰ)f (x)= •
• =(cos2x,1)•(1,
=(cos2x,1)•(1, sin2x)
sin2x)
= sin2x+cos2x
sin2x+cos2x
=2 sin(2x+ ),…(6分)
),…(6分)
∴最小正周期T= ,
,
令2x+ =k
=k ,k∈Z,解得x=
,k∈Z,解得x=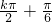 ,k∈Z,
,k∈Z,
即f (x)的对称轴方程为x=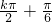 ,k∈Z.…(8分)
,k∈Z.…(8分)
(Ⅱ)当x∈[0, ]时,即0≤x≤
]时,即0≤x≤ ,可得
,可得 ≤2x+
≤2x+ ≤
≤ ,
,
∴当2x+ =
= ,即x=
,即x= 时,f (x)取得最大值f (
时,f (x)取得最大值f ( )=2;
)=2;
当2x+ =
= ,即x=
,即x= 时,f (x)取得最小值f (
时,f (x)取得最小值f ( )=-1.
)=-1.
即f (x) 的值域为[-1,2].…(12分)
分析:(Ⅰ)通过向量的数量积,利用两角和的正弦函数,化简函数为一个角的一个三角函数的形式,即可求出函数f(x)的最小正周期及对称轴方程.
(Ⅱ)通过x的范围求出2x+ 的范围,利用正弦函数的值域,求解函数的值域即可.
的范围,利用正弦函数的值域,求解函数的值域即可.
点评:本题以向量为依托,考查三角函数的两角和的正弦函数的应用,函数的周期,值域的求法,考查计算能力.
 •
• =(cos2x,1)•(1,
=(cos2x,1)•(1, sin2x)
sin2x)=
 sin2x+cos2x
sin2x+cos2x=2 sin(2x+
 ),…(6分)
),…(6分)∴最小正周期T=
 ,
,令2x+
 =k
=k ,k∈Z,解得x=
,k∈Z,解得x=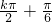 ,k∈Z,
,k∈Z,即f (x)的对称轴方程为x=
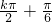 ,k∈Z.…(8分)
,k∈Z.…(8分)(Ⅱ)当x∈[0,
 ]时,即0≤x≤
]时,即0≤x≤ ,可得
,可得 ≤2x+
≤2x+ ≤
≤ ,
,∴当2x+
 =
= ,即x=
,即x= 时,f (x)取得最大值f (
时,f (x)取得最大值f ( )=2;
)=2;当2x+
 =
= ,即x=
,即x= 时,f (x)取得最小值f (
时,f (x)取得最小值f ( )=-1.
)=-1.即f (x) 的值域为[-1,2].…(12分)
分析:(Ⅰ)通过向量的数量积,利用两角和的正弦函数,化简函数为一个角的一个三角函数的形式,即可求出函数f(x)的最小正周期及对称轴方程.
(Ⅱ)通过x的范围求出2x+
 的范围,利用正弦函数的值域,求解函数的值域即可.
的范围,利用正弦函数的值域,求解函数的值域即可.点评:本题以向量为依托,考查三角函数的两角和的正弦函数的应用,函数的周期,值域的求法,考查计算能力.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
设向量
=(cos2x,sin2x),
=(cos2x,-sin2x),函数f(x)=
•
,则函数f(x)的图象( )
| a |
| b |
| a |
| b |
| A、关于点(π,0)中心对称 | ||
B、关于点(
| ||
C、关于点(
| ||
| D、关于点(0,0)中心对称 |