题目内容
从数列 中抽出一些项,依原来的顺序组成的新数列叫数列
中抽出一些项,依原来的顺序组成的新数列叫数列 的一个子列.
的一个子列.
(1)写出数列 的一个是等比数列的子列;
的一个是等比数列的子列;
(2)设 是无穷等比数列,首项
是无穷等比数列,首项 ,公比为
,公比为 .求证:当
.求证:当 时,数列
时,数列 不存在
不存在
是无穷等差数列的子列.
 中抽出一些项,依原来的顺序组成的新数列叫数列
中抽出一些项,依原来的顺序组成的新数列叫数列 的一个子列.
的一个子列.(1)写出数列
 的一个是等比数列的子列;
的一个是等比数列的子列;(2)设
 是无穷等比数列,首项
是无穷等比数列,首项 ,公比为
,公比为 .求证:当
.求证:当 时,数列
时,数列 不存在
不存在是无穷等差数列的子列.
(1)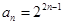 ;(2)证明过程详见解析.
;(2)证明过程详见解析.
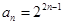 ;(2)证明过程详见解析.
;(2)证明过程详见解析.试题分析:本题主要考查等差数列、等比数列的定义、通项公式及其性质等基础知识,考查学生的分析问题解决问题的能力、转化能力、逻辑推理能力.第一问,在数列
 的所有项中任意抽取几项,令其构成等比数列即可,但是至少抽取3项;第二问,分2种情况进行讨论:
的所有项中任意抽取几项,令其构成等比数列即可,但是至少抽取3项;第二问,分2种情况进行讨论: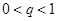 和
和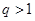 ,利用数列的单调性,先假设存在,在推导过程中找出矛盾即可.
,利用数列的单调性,先假设存在,在推导过程中找出矛盾即可.试题解析:(1)
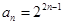 (若只写出2,8,32三项也给满分). 4分
(若只写出2,8,32三项也给满分). 4分(2)证明:假设能抽出一个子列为无穷等差数列,设为
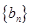 ,通项公式为
,通项公式为 .因为
.因为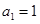
所以
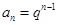 .
.(1)当
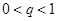 时,
时,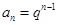 ∈(0,1],且数列
∈(0,1],且数列 是递减数列,
是递减数列,所以
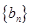 也为递减数列且
也为递减数列且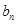 ∈(0,1],
∈(0,1],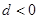 ,
,令
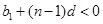 ,得
,得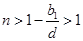 ,
,即存在
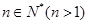 使得
使得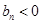 ,这与
,这与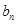 ∈(0,1]矛盾.
∈(0,1]矛盾.(2)当
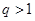 时,
时,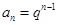 ≥1,数列
≥1,数列 是递增数列,
是递增数列,所以
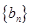 也为递增数列且
也为递增数列且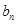 ≥1,
≥1,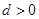 .
.因为d为正的常数,且
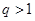 ,
,所以存在正整数m使得
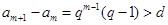 .
.令
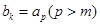 ,则
,则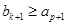 ,
,因为
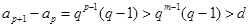 =
=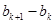 ,
,所以
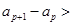
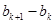 ,即
,即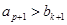 ,但这与
,但这与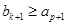 矛盾,说明假设不成立.
矛盾,说明假设不成立.综上,所以数列
 不存在是无穷等差数列的子列. 13分
不存在是无穷等差数列的子列. 13分
练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 中,
中, 其前
其前 项和
项和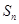 满足:
满足:

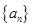 满足:
满足: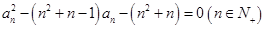 ,数列
,数列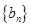 的前
的前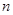 项和为
项和为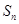 ,且满足
,且满足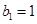 ,
,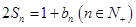 .
.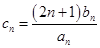 ,数列
,数列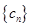 的前
的前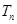 ,求证:
,求证: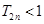 .
.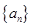 中,
中,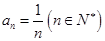 .从数列
.从数列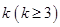 项并按原顺序组成的新数列记为
项并按原顺序组成的新数列记为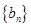 ,并称
,并称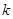 项子列.例如数列
项子列.例如数列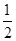 、
、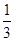 、
、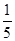 、
、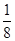 为
为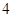 项子列.
项子列.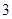 项子列,并使其为等差数列;
项子列,并使其为等差数列;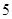 项子列,且
项子列,且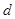 满足
满足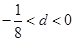 ;
;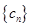 为数列
为数列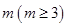 项子列,且
项子列,且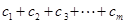
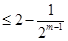 .
.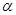 为锐角,且
为锐角,且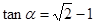 ,函数
,函数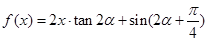 ,数列
,数列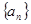 的首项
的首项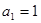 ,
,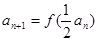 .
. 的表达式;(2)求数列
的表达式;(2)求数列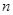 项和
项和 .
.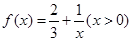 ,数列
,数列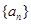 满足
满足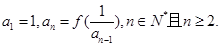
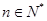 ,设
,设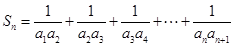 ,若
,若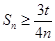 恒成立,求实数
恒成立,求实数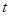 的取值范围.
的取值范围. ,在验证n=1成立时,等式左边是
,在验证n=1成立时,等式左边是 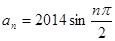 ,则
,则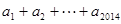 =( )
=( )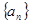 中,
中,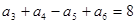 ,则
,则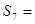 ( )
( )