题目内容
已知正项数列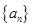 满足:
满足: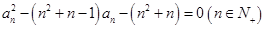 ,数列
,数列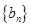 的前
的前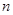 项和为
项和为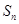 ,且满足
,且满足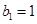 ,
,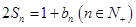 .
.
(1)求数列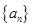 和
和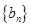 的通项公式;
的通项公式;
(2)设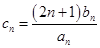 ,数列
,数列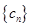 的前
的前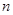 项和为
项和为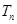 ,求证:
,求证: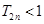 .
.
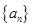 满足:
满足: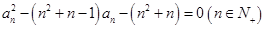 ,数列
,数列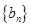 的前
的前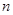 项和为
项和为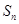 ,且满足
,且满足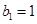 ,
,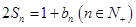 .
.(1)求数列
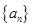 和
和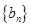 的通项公式;
的通项公式;(2)设
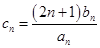 ,数列
,数列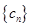 的前
的前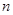 项和为
项和为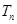 ,求证:
,求证: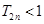 .
.(1)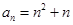 ,
,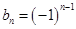 ;(2)详见解析.
;(2)详见解析.
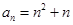 ,
,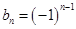 ;(2)详见解析.
;(2)详见解析.试题分析:(1)解以
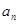 为变量的一元二次方程得出数列
为变量的一元二次方程得出数列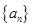 的通项公式,利用
的通项公式,利用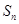 与
与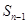 之间的关系利用作差法求出数列
之间的关系利用作差法求出数列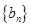 的通项公式;(2)先求出数列
的通项公式;(2)先求出数列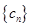 的通项公式,方法一是将
的通项公式,方法一是将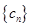 的前
的前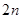 项和中的项一一配对并进行裂项展开,然后利用裂项法求
项和中的项一一配对并进行裂项展开,然后利用裂项法求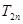 ,进而证明相应不等式;方法二是将数列
,进而证明相应不等式;方法二是将数列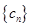 中的每一项进行拆开,然后逐项求和
中的每一项进行拆开,然后逐项求和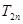 ,进而证明相应不等式.
,进而证明相应不等式.试题解析:(1)由
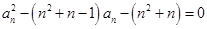 ,得
,得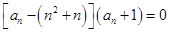 ,
,由于
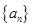 是正项数列,所以
是正项数列,所以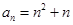 ,
,由
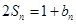 可得当
可得当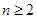 时,
时,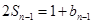 ,两式相减得
,两式相减得 ,
,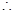 数列
数列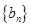 是首项为
是首项为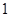 ,公比
,公比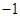 的等比数列,
的等比数列,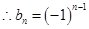 ;
;(2)
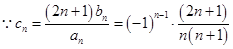 ,
,方法一:
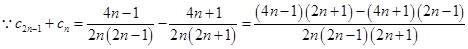
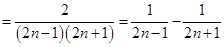 ,
,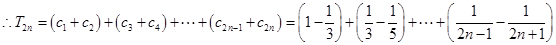
 ;
;方法二:
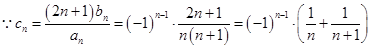 ,
,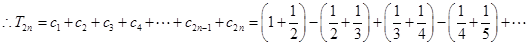
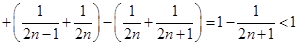 .
.
练习册系列答案
相关题目
 是公差不为零的等差数列,
是公差不为零的等差数列, ,且
,且 是
是 和
和 的等比中项,求:
的等比中项,求: .
. 中抽出一些项,依原来的顺序组成的新数列叫数列
中抽出一些项,依原来的顺序组成的新数列叫数列 的一个是等比数列的子列;
的一个是等比数列的子列; ,公比为
,公比为 .求证:当
.求证:当 时,数列
时,数列 的通项公式为
的通项公式为 ,下列四个命题.
,下列四个命题. :数列
:数列 :数列
:数列 是递增数列;
是递增数列; :数列
:数列 是递增数列;
是递增数列; :数列
:数列 是递增数列.其中真命题的是 .
是递增数列.其中真命题的是 . 个“金鱼”图需要火柴棒的根数为( )
个“金鱼”图需要火柴棒的根数为( )




 中,如果
中,如果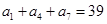 ,
,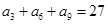 ,则数列
,则数列 是等差数列
是等差数列 的前
的前 项和,若
项和,若 ,则
,则 ( )
( )
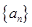 中,
中,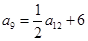 ,则数列
,则数列 是等差数列
是等差数列 的前
的前 项和,
项和, ,则
,则 的值为( )
的值为( )


