Question

17．${∫}_{0}^{1}$e^xdx与${∫}_{0}^{1}$e${\;}^{{x}^{2}}$dx的关系为（　　）

• A． ${∫}_{0}^{1}$e^xdx＜${∫}_{0}^{1}$e${\;}^{{x}^{2}}$dx
• B． ${∫}_{0}^{1}$e^xdx＞${∫}_{0}^{1}$e${\;}^{{x}^{2}}$dx
• C． （${∫}_{0}^{1}$e^xdx）²=${∫}_{0}^{1}$e${\;}^{{x}^{2}}$dx
• D． $\frac{1}{2}$${∫}_{0}^{1}$e^xdx=${∫}_{0}^{1}$e${\;}^{{x}^{2}}$dx

Answer 1

分析 根据积分所表示的几何意义是以直线x=0，x=1及函数y=e^x或y=${e}^{{x}^{2}}$在图象第一象限内圆弧与坐标轴围成的面积，只需画出函数图象观察面积大小即可．

解答 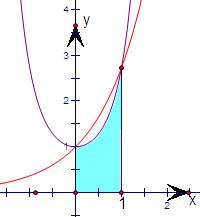解：∫₀¹e^xdx表示的几何意义是以直线x=0，x=1及函数y=e^x在图象第一象限内圆弧与坐标轴围成的面积，
∫₀¹${e}^{{x}^{2}}$dx表示的几何意义是以直线x=0，x=1及函数y=${e}^{{x}^{2}}$在图象第一象限内圆弧与坐标轴围成的面积，
如图
∵当0＜x＜1时，e^x＞${e}^{{x}^{2}}$，故有：∫₀¹e^xdx＞∫₀¹=${e}^{{x}^{2}}$dx
故选：B．

点评 本题主要考查了定积分，定积分运算是求导的逆运算，解题的关键是求原函数，也可利用几何意义进行求解，属于基础题．