题目内容
20.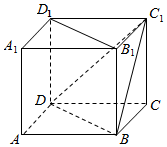 如图,ABCD-A1B1C1D1为正方体.
如图,ABCD-A1B1C1D1为正方体.(1)求证:B1D1∥平面BC1D;
(2)求异面直线B1D1与BC1所成角的大小;
(3)求证BD⊥平面ACC1.
分析 (1)由B1D1∥BD,能证明B1D1∥平面BC1D.
(2)由B1D1∥BD,得∠DBC1是异面直线B1D1与BC1所成角,由此能求出异面直线B1D1与BC1所成角.
(3)推导出BD⊥CC1,AC⊥BD,由此能证明BD⊥平面ACC1.
解答 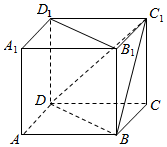 证明:(1)∵ABCD-A1B1C1D1为正方体,
证明:(1)∵ABCD-A1B1C1D1为正方体,
∴B1D1∥BD,
∵B1D1?平面BC1D,BD?平面BC1D
∴B1D1∥平面BC1D.
解:(2)∵B1D1∥BD,∴∠DBC1是异面直线B1D1与BC1所成角,
∵BD=BC1=DC1,
∴∠DBC1=60°,
∴异面直线B1D1与BC1所成角为60°.
证明:(3)∵ABCD-A1B1C1D1为正方体,
∴ABCD是正方形,BD⊥CC1,∴AC⊥BD,
∵AC∩CC1=C,∴BD⊥平面ACC1.
点评 本题考查线面平行的证明,考查异面直线所成角的求法,考查线面垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
11.已知l、m、n是空间不同的三条直线,则下列结论中正确的( )
| A. | 若m⊥l,n⊥l,则m⊥n | B. | 若m⊥l,n⊥l,则m∥n | C. | 若m⊥l,n∥l,则m⊥n | D. | 若m⊥l,n∥l,则m∥n |
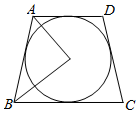 一个圆内切于一个等腰锑形,已知圆面积是等腰锑形面积的$\frac{1}{2}$,求等腰梯形的底角(用反正切表示)
一个圆内切于一个等腰锑形,已知圆面积是等腰锑形面积的$\frac{1}{2}$,求等腰梯形的底角(用反正切表示)