题目内容
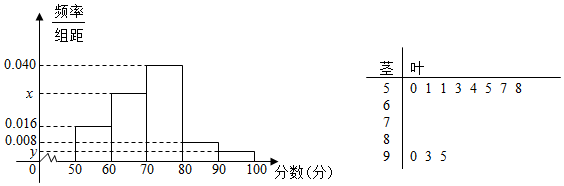
6.某校为了了解学生的数学期中考试成绩,从中抽取部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在[50,60),[90,100]的数据).(Ⅰ)求样本容量n和频率分布直方图中的x、y的值;
(Ⅱ)在选取的样本中,从成绩在80分以上(含80分)的学生中随机抽取2名同学到市里参加数学竞赛,求这2人的成绩均在[90,100]内的概率.
分析 (Ⅰ)由样本容量和频数频率的关系易得答案;
(Ⅱ)由题意可知,分数在[80,90)内的学生有5人,记这5人分别为a1,a2,a3,a4,a5,分数在[90,100]内的学生有2人,记这2人分别为b1,b2,列举法易得.
解答 解:(Ⅰ)由题意可知,样本容量n=$\frac{8}{0.016×10}$=50,(2分)y=$\frac{2}{50×10}$=0.004,…(4分)
x=0.100-0.004-0.010-0.016-0.040=0.030.(6分)
(Ⅱ)由题意可知,分数在[80,90]内的学生有5人,记这5人分别为a1,a2,a3,a4,a5,分数在[90,100]内的学生有2人,记这2人分别为b1,b2,
抽取2名学生的所有情况有21种,分别为:(a1,a2),(a1,a3),(a1,a4),(a1,a5),(a1,b1),(a1,b2),(a2,a3),(a2,a4),(a2,a5),(a2,b1),(a2,b2),(a3,a4),(a3,a5),(a3,b1),(a3,b2),(a4,a5),(a4,b1),(a4,b2),(a5,b1),(a5,b2),(b1,b2).(8分)
这2人的成绩均在[90,100]内有1种,(10分)
∴所抽取的2名学生中恰有一人得分在[90,100]内的概率$\frac{1}{21}$.(12分)
点评 本小题主要考查茎叶图、样本均值、样本方差、概率等知识,考查或然与必然的数学思想方法,以及数据处理能力、运算求解能力和应用意识.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}<$φ<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{π}{3}$)=( )


| A. | $\sqrt{3}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
15.已知等比数列{an}的前n项和为Sn,a1+a3=$\frac{5}{8}$,S4=$\frac{5}{4}$,则数列{an}的公比为( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{2}$ | C. | $\frac{7}{8}$ | D. | 1 |
7.已知双曲线C与双曲线$\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{27}$=1有共同的渐近线,并且经过点A(3,-6$\sqrt{2}$),F1,F2是双曲线C的左、右焦点,若点P在双曲线C上,且∠F1PF2=90°,则|$\overrightarrow{P{F}_{1}}$+$\overrightarrow{P{F}_{2}}$|等于( )
| A. | 2$\sqrt{5}$ | B. | $\sqrt{5}$ | C. | 2$\sqrt{10}$ | D. | $\sqrt{10}$ |
 环保组织随机抽检市内某河流2015年内100天的水质,检测单位体积河水中重金属含量x,并根据抽检数据绘制了如下图所示的频率分布直方图.
环保组织随机抽检市内某河流2015年内100天的水质,检测单位体积河水中重金属含量x,并根据抽检数据绘制了如下图所示的频率分布直方图.