题目内容
10.在直角坐标系中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为ρ2-4ρcosθ+1=0,直线l的参数方程为$\left\{\begin{array}{l}x=3+\sqrt{3}t\\ y=\sqrt{3}+t\end{array}\right.$(t为参数),点A的极坐标为$({2\sqrt{3},\frac{π}{6}})$,设直线l与曲线C相交于P,Q两点.(1)写出曲线C的直角坐标方程和直线l的普通方程;
(2)求|AP|•|AQ|•|OP|•|OQ|的值.
分析 (1)利用三种方程的转化方法,写出曲线C的直角坐标方程和直线l的普通方程;
(2)将参数方程标准式$\left\{\begin{array}{l}x=3+\frac{{\sqrt{3}t}}{2}\\ y=\sqrt{3}+\frac{t}{2}\end{array}\right.(t为参数)$与(x-2)2+y2=3联立得${t^2}+2\sqrt{3}t+1=0$,由韦达定理得:t1t2=1,|AP||AQ|=1;将直线$θ=\frac{π}{6}(ρ∈R)$的极坐标方程与圆的极坐标方程ρ2-4ρcosθ+1=0,联立得:${ρ^2}-2\sqrt{3}ρ+1=0$,由韦达定理得:ρ1ρ2=1,即|OP||OQ|=1,即可求|AP|•|AQ|•|OP|•|OQ|的值.
解答 解:(1)曲线C的直角坐标方程为:x2+y2-4x+1=0,即(x-2)2+y2=3…2分
直线的普通方程为$x-\sqrt{3}y=0$…4分
(2)点A的直角坐标为$(3,\sqrt{3})$,设点P,Q对应的参数为t1,t2,
点P,Q的极坐标方程为$({ρ_1},\frac{π}{6})Q({ρ_2},\frac{π}{6})$,
将参数方程标准式$\left\{\begin{array}{l}x=3+\frac{{\sqrt{3}t}}{2}\\ y=\sqrt{3}+\frac{t}{2}\end{array}\right.(t为参数)$与(x-2)2+y2=3联立得${t^2}+2\sqrt{3}t+1=0$,
由韦达定理得:t1t2=1,|AP||AQ|=1…6分,
将直线$θ=\frac{π}{6}(ρ∈R)$的极坐标方程与圆的极坐标方程ρ2-4ρcosθ+1=0
联立得:${ρ^2}-2\sqrt{3}ρ+1=0$,由韦达定理得:ρ1ρ2=1,即|OP||OQ|=1…8分,
所以,|AQ||AP||OP||OQ|=1…10分.
点评 本题考查三种方程的转化,考查参数方程、极坐标方程的运用,正确转化是关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案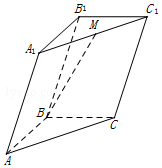
| A. | $-\frac{1}{2}\vec a+\frac{1}{2}\vec b+\vec c$ | B. | $\frac{1}{2}\vec a+\frac{1}{2}\vec b+\vec c$ | C. | $-\frac{1}{2}\vec a-\frac{1}{2}\vec b+\vec c$ | D. | $\frac{1}{2}\vec a-\frac{1}{2}\vec b+\vec c$ |
| A. | 12斤 | B. | 15斤 | C. | 15.5斤 | D. | 18斤 |
| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 4 |
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{5}{4}$ | D. | 5 |

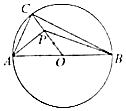 如图,AB为圆O的直径且AB=4,C为圆上不同于A、B的任意一点,若P为半径OC上的动点,则($\overrightarrow{PA}$+$\overrightarrow{PB}$)•$\overrightarrow{PC}$的最小值是( )
如图,AB为圆O的直径且AB=4,C为圆上不同于A、B的任意一点,若P为半径OC上的动点,则($\overrightarrow{PA}$+$\overrightarrow{PB}$)•$\overrightarrow{PC}$的最小值是( )