题目内容
【题目】已知椭圆
，圆
（
为坐标原点）.过点
且斜率为
的直线与圆交于点
，与椭圆
的另一个交点的横坐标为
.
（1）求椭圆的方程和圆的方程；
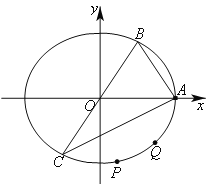
（2）过圆上的动点
作两条互相垂直的直线
，
，若直线的斜率为
且与椭圆相切，试判断直线与椭圆的位置关系，并说明理由.
【答案】（1）
；
（2）直线
与椭圆
相切，详见解析
【解析】
（1）根据圆
过点
可得圆的方程为：，根据过点
且斜率为
的直线过点，可得
，可得直线与椭圆相交的另一个交点坐标为
，将其代入椭圆方程可得椭圆的方程为；
（2）设圆上的动点
，所以
，设直线
：
，将其代入，得
，利用判别式为0，可得
，设直线：
，将其代入，利用判别式为0可证直线与椭圆相切.
（1）因为圆过点，所以圆的方程为：.
因为过点且斜率为的直线方程为
，
又因为过点，所以.
因为直线与椭圆相交的另一个交点坐标为，
所以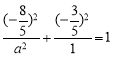
，解得
.
所以椭圆的方程为.
（2）直线与椭圆相切.理由如下：
设圆上的动点，所以.
依题意，设直线：.
由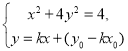
得.
因为直线与椭圆相切，
所以
.
所以
.
所以
.
因为，所以
.
所以.
设直线：，
由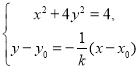
得
.
则
.
所以直线与椭圆相切.
【题目】某商场为迎接“618年中庆典，拟推出促销活动，活动规则如下：①活动期间凡在商场内购物，每满673元可参与一次现金红包抽奖，且互不影响，详细如下表：
奖项 | 一等奖 | 二等奖 |
奖金 | 200元现金红包 | 优惠餐券1张（价值50元） |
获奖率 | 30% | 70% |
②活动期间凡在商场内购物，每满2019元可参与消费返现，返现金额为实际消费金额的15%.规定每位顾客只可选择参加其中一种优惠活动.
（1）现有顾客甲在商场消费2019元，若其选择参与抽奖，求其可以获得现金红包的概率.
（2）现有100名消费金额为2019元的顾客正在等待抽奖，假如你是该商场的活动策划人，你更希望顾客参与哪项优惠活动？
【题目】呼和浩特市地铁一号线于2019年12月29日开始正式运营有关部门通过价格听证会，拟定地铁票价后又进行了一次调查.调查随机抽查了50人，他们的月收入情况与对地铁票价格态度如下表：
月收入（单位：百元） |
|
|
|
|
|
|
认为票价合理的人数 | 1 | 2 | 3 | 5 | 3 | 4 |
认为票价偏高的人数 | 4 | 8 | 12 | 5 | 2 | 1 |
（1）若以区间的中点值作为月收入在该区间内人的人均月收入求参与调查的人员中“认为票价合理者”的月平均收入与“认为票价偏高者”的月平均收入的差是多少（结果保留2位小数）；
（2）由以上统计数据填写下面
列联表分析是否有
的把握认为“月收入以5500元为分界点对地铁票价的态度有差异”
月收入不低于5500元人数 | 月收入低于5500元人数 | 合计 | |
认为票价偏高者 | |||
认为票价合理者 | |||
合计 |
附：
| 0.05 | 0.01 |
| 3.841 | 6.635 |
