题目内容
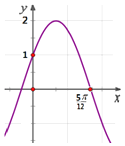
【题目】函数![]() 的部分图象如图所示,则下列叙述正确的是( )
的部分图象如图所示,则下列叙述正确的是( )
A.函数![]() 的图象可由
的图象可由![]() 的图象向左平移
的图象向左平移![]() 个单位得到
个单位得到
B.函数![]() 的图象关于直线
的图象关于直线![]() 对称
对称
C.函数![]() 在区间
在区间![]() 上是单调递增的
上是单调递增的
D.函数![]() 图象的对称中心为
图象的对称中心为![]()
【答案】D
【解析】
根据题意求出解析式,利用正弦函数的对称性及单调性依次判断选项.
由图象可知A=2,f(0)=1,
∵f(0)=2sinφ=1,且![]() ,
,
∴![]() ,
,
∴f(x)=2sin(ωx![]() ),
),
∵f(![]() )=0且为单调递减时的零点,
)=0且为单调递减时的零点,
∴![]() ,k∈Z,
,k∈Z,
∴![]() ,k∈Z,
,k∈Z,
由图象知![]() ,
,
∴ω![]() ,
,
又∵ω>0,
∴ω=2,
∴f(x)=2sin(2x![]() ),
),
∵函数f(x)的图象可由y=Asinωx的图象向左平移![]() 个单位得,
个单位得,
∴A错,
令2x![]() ,k∈Z,对称轴为x
,k∈Z,对称轴为x![]() ,则B错,
,则B错,
令2x![]() ,则x
,则x![]() ,则C错,
,则C错,
令2x![]() kπ,k∈Z,则x=
kπ,k∈Z,则x=![]() ,则D对,
,则D对,
故选:D.

练习册系列答案
相关题目