题目内容
14.已知b>0,直线x-b2y-1=0与直线(3b2+1)x+ay+2=0互相垂直,则ab最小值等于( )| A. | 1 | B. | 2 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
分析 利用相互垂直的直线与斜率之间的关系可得ab2=3b2+1.再利用基本不等式的性质即可得出.
解答 解:直线x-b2y-1=0与直线(3b2+1)x+ay+2=0互相垂直,
∴3b2+1-ab2=0,
化为ab2=3b2+1.
∴ab=3b+$\frac{1}{b}$≥2$\sqrt{3b•\frac{1}{b}}$=2$\sqrt{3}$,当且仅当b=$\frac{\sqrt{3}}{3}$时取等号.
∴ab的最小值为2$\sqrt{3}$.
故选:D.
点评 本题考查了相互垂直的直线与斜率之间的关系、基本不等式的性质,属于基础题.

练习册系列答案
相关题目
3.不等式x(x-1)≥x的解集为( )
| A. | {x|x≤0或x≥2} | B. | {x|0≤x≤2} | C. | {x|x≥2} | D. | {x|x≤0或x≥1} |
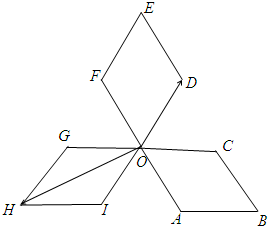 如图,四边形OABC,ODEF,OGHI是三个全等的菱形,∠COD=∠FOG=∠AOI=60°,P为各菱形边上的动点,设$\overrightarrow{OP}$=x$\overrightarrow{OD}$+y$\overrightarrow{OH}$,则x+y的最大值为( )
如图,四边形OABC,ODEF,OGHI是三个全等的菱形,∠COD=∠FOG=∠AOI=60°,P为各菱形边上的动点,设$\overrightarrow{OP}$=x$\overrightarrow{OD}$+y$\overrightarrow{OH}$,则x+y的最大值为( ) 如图圆O是半径为1的圆,点PO、P1、P2、P3将圆4等分,则$\overrightarrow{O{P}_{0}}$$•\overrightarrow{O{P}_{i}}$(i=0,1,2,3)的取值集合是{-1,0,1}.
如图圆O是半径为1的圆,点PO、P1、P2、P3将圆4等分,则$\overrightarrow{O{P}_{0}}$$•\overrightarrow{O{P}_{i}}$(i=0,1,2,3)的取值集合是{-1,0,1}.