题目内容
如图，在△OAB中，已知|| OA |
| OB |
| 3 |
| AD |
| AB |
（1）若
| OD |
| 3 |
| 4 |
| OA |
| 1 |
| 4 |
| OB |
（2）若
| OC |
| OP |
| OD |
| OC |
| OP |
分析：（1）由题意，可得
=
+
=
+λ
，再将
表示为(1-λ)
+λ
，于是由平面向量基本定理可以得出λ所满足的方程，解出它的值；
（2）由题意，可O为原点，OA为x轴，OB为y轴建立直角坐标系，利用向量的坐标运算求出两向量
，
的坐标，再由向量的数量积运算求出
•
的值．
| OD |
| OA |
| AD |
| OA |
| AB |
| OD |
| OA |
| OB |
（2）由题意，可O为原点，OA为x轴，OB为y轴建立直角坐标系，利用向量的坐标运算求出两向量
| OC |
| OP |
| OC |
| OP |
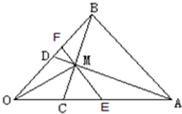
解答：解：（1）由题意，如图
=
+λ(
-
)=(1-λ)
+λ
又
=
+
∴λ=
（2）以O为原点，OA为x轴，OB为y轴建立直角坐标系
记∠POA=α则P(cosα，sinα)，A(2，0)，B(0，2
)，C(1，0)
=
+λ
=(2(1-λ)，2
λ)
由
+
=
得
整理得16λ2-4λ=0解得λ=0（舍），λ=
∴
=
-
=(
，
)-(1，0)=(
，
)
则
•
=
…（2分）
|
| OA |
| OB |
| OA |
| OA |
| OB |
又
| OD |
| 3 |
| 4 |
| OA |
| 1 |
| 4 |
| OB |
∴λ=
| 1 |
| 4 |
（2）以O为原点，OA为x轴，OB为y轴建立直角坐标系
记∠POA=α则P(cosα，sinα)，A(2，0)，B(0，2
| 3 |
| OD |
| OA |
| AB |
| 3 |
由
| OC |
| OP |
| OD |
得
|
| 1 |
| 4 |
∴
| OP |
| OD |
| OC |
| 3 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
则
| OC |
| OP |
| 1 |
| 2 |
点评：本题考点为向量在几何中的应用，考查平面向量基本定理，向量的数量积表示，向量的线性运算，解题的关键是理解题意，选择恰当的方法求值，第一小题关键是理解平面向量基本定理的意义，由在基底上的分解是唯一的得出参数的方程求参数，第二小题关键是依据题设条件建立坐标系，利用向量的坐标表示计算两向量的内积，本题考察了议程的思想，数形结合的思想，是向量中经典题型
练习册系列答案
阅读快车系列答案
相关题目
如图，在△OAB中，
（2013•杭州二模）如图，在△OAB中，C为OA上的一点，且
如图，在△OAB中，已知
如图，在△OAB中，延长BA到C，使AC=BA，在OB上取点D，使DB=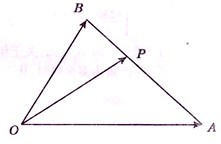
如图，在△OAB中，已知P为线段AB上的一点，且|