题目内容
已知函数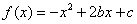 ,设函数
,设函数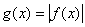 在区间
在区间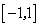 上的最大值为
上的最大值为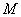 .
.
(Ⅰ)若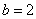 ,试求出
,试求出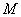 ;
;
(Ⅱ)若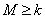 对任意的
对任意的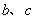 恒成立,试求
恒成立,试求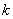 的最大值.
的最大值.
解:(Ⅰ)当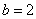 时
时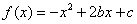 在区间
在区间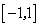 上是增函数,
上是增函数,
则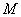 是
是 和
和 中较大的一个, ………………………2分
中较大的一个, ………………………2分
又
 ,
,
 ,则
,则 …………………4分
…………………4分
(Ⅱ)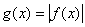

(i)当 时,
时, 在区间
在区间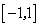 上是单调函数,则
上是单调函数,则
而
 ,
,
 ,
,
则



 ,可知
,可知 ……………6分
……………6分
(ii)当 时,函数
时,函数 的对称轴
的对称轴 位于区间
位于区间 之内,
之内,
此时 ,又
,又 , …………8分
, …………8分
① 当 时,有
时,有 ,
,
则




 ………………………10分
………………………10分
② 当 时,有
时,有 ,
,
则




 …………………………12分
…………………………12分
综上可知,对任意的 、
、 都有
都有
而当 ,
, 时,
时, 在区间
在区间 上的最大值
上的最大值 ,故
,故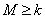 对任意的
对任意的 、
、 恒成立的
恒成立的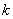 的最大值为
的最大值为

练习册系列答案
相关题目
 和
和 ,其中
,其中 为实数.若
为实数.若 ,则
,则 的取值范围是
的取值范围是  满足
满足 ,
, ,
, ,则
,则 的最大值等于 ( )
的最大值等于 ( ) C.
C. D.1
D.1  ,B=
,B= ,则A∩B= ,
,则A∩B= , = , = .
= , = . ,则
,则 的
的  成角的正弦值为( )
成角的正弦值为( )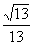 B.
B. 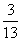 C.
C. 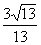 D.
D.
 的最小值为 ;若ax2﹣4x+c>0的解集为 (-1,2),则
的最小值为 ;若ax2﹣4x+c>0的解集为 (-1,2),则 =
=  的最大值为 ,最小正周期为 ,在
的最大值为 ,最小正周期为 ,在 上的值域为
上的值域为  的值为 .
的值为 .