题目内容
在Rt△ABC中,∠CAB=90°,AB=2,AC=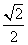 ,一曲线E过C点,动点P在曲线E上运动,且保持|PA|+|PB|的值不变.
,一曲线E过C点,动点P在曲线E上运动,且保持|PA|+|PB|的值不变.
(1)建立适当的坐标系,求曲线E的方程;
(2)直线l:y=x+t与曲线E交于M,N两点,求四边形MANB的面积的最大值.
解 (1)以AB为x轴,以AB中点为原点O建立直角坐标系,∵|PA|+|PB|=|CA|+|CB|

 所以四边形MANB的面积最大值是
所以四边形MANB的面积最大值是 .
.

练习册系列答案
相关题目
下面是2×2列联表:
|
| y1 | y2 | 总计 |
| x1 | a | 21 | 73 |
| x2 | 22 | 25 | 47 |
| 总计 | b | 46 | 120 |
则表中a,b的值分别为( )
A.94,72 B.52,50
C.52,74 D.74,52
 -
-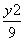 =1上,则
=1上,则 为( )
为( ) B.
B.
 D.
D.
 +y
+y 的最小值是________.
的最小值是________. (O为原点),其中λ1,λ2∈R,且λ1+λ2=1,则点C的轨迹是( )
(O为原点),其中λ1,λ2∈R,且λ1+λ2=1,则点C的轨迹是( ) =1与椭圆x2+
=1与椭圆x2+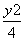 =1交于A,B两点,O为原点,则△OAB的面积为________.
=1交于A,B两点,O为原点,则△OAB的面积为________.