题目内容
已知α∈(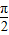 ,π),向量
,π),向量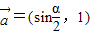 ,
,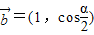 ,且
,且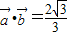
(1)求cosα的值;
(2)若sin(α+β)=-
 ,β∈(0,
,β∈(0,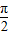 ),求sinβ的值.
),求sinβ的值.
【答案】分析:(1)利用向量的数量积、同角三角函数的平方关系、倍角公式即可得出;
(2)利用平方关系、两角和的正弦关系即可得出.
解答:解:(1)∵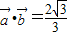 ,∴
,∴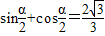 ,
,
两边平方得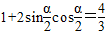 ,∴
,∴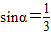 .
.
∵α∈(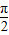 ,π),∴
,π),∴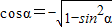 =-
=-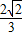 .
.
(2)∵α∈(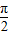 ,π),β∈(0,
,π),β∈(0,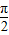 ),
),
∴ .
.
∵sin(α+β)=- ,
,
∴cos(α+β)=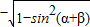 =-
=- .
.
∴sinβ=sin[(α+β)-α]=sin(α+β)cosα-cos(α+β)sinα
=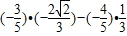
=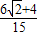 .
.
点评:熟练掌握向量的数量积、同角三角函数的平方关系、倍角公式、两角和的正弦关系等是解题的关键.
(2)利用平方关系、两角和的正弦关系即可得出.
解答:解:(1)∵
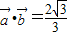 ,∴
,∴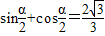 ,
,两边平方得
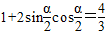 ,∴
,∴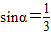 .
.∵α∈(
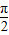 ,π),∴
,π),∴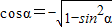 =-
=-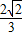 .
.(2)∵α∈(
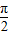 ,π),β∈(0,
,π),β∈(0,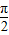 ),
),∴
 .
.∵sin(α+β)=-
 ,
,∴cos(α+β)=
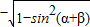 =-
=- .
.∴sinβ=sin[(α+β)-α]=sin(α+β)cosα-cos(α+β)sinα
=
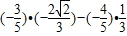
=
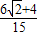 .
.点评:熟练掌握向量的数量积、同角三角函数的平方关系、倍角公式、两角和的正弦关系等是解题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时向左、右两边下落的概率都是
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时向左、右两边下落的概率都是 (2012•信阳模拟)将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落,小球在下落的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中,已知小球每次遇到障碍物时,向左、右两边下落的概率都是
(2012•信阳模拟)将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落,小球在下落的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中,已知小球每次遇到障碍物时,向左、右两边下落的概率都是 ,将其图象向左移
,将其图象向左移 个单位,并向上移
个单位,并向上移 个单位,得到函数
个单位,得到函数 的图象.
的图象. 的值;
的值; ,求函数
,求函数 的单调递增区间和最值.
的单调递增区间和最值. 袋或
袋或 袋中.已知小球每次遇到黑色障碍物时向左、右两边下落的概率都是.
袋中.已知小球每次遇到黑色障碍物时向左、右两边下落的概率都是. ;
; 为落入
为落入 的概率和
的概率和 .
.