题目内容
已知a∈R，x＞0，y＞0，且x+y=1，则“a≤8”是“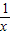
+
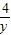≥a恒成立”的（ ）A．充分不必要条件
B．必要不充分条件
C．充要条件
D．既不充分也不必要条件
【答案】分析：利用基本不等式可得“
+
≥a恒成立”等价于a≤9，再根据{a|a≤8}?{a|a≤9}，从而得出结论．
解答：解：∵已知a∈R，x＞0，y＞0，且x+y=1，
∴
+
=（x+y）（
+
）=5+
+
≥9，当且仅当 x=
且 y=
时，取等号．
故“
+
≥a恒成立”等价于a≤9．
而{a|a≤8}?{a|a≤9}，故“a≤8”是“
+
≥a恒成立”的充分不必要条件，
故选A．
点评：本题主要考查充分条件、必要条件、充要条件的定义，基本不等式的应用，体现了等价转化的数学思想，
属于基础题．
+≥a恒成立”等价于a≤9，再根据{a|a≤8}?{a|a≤9}，从而得出结论．解答：解：∵已知a∈R，x＞0，y＞0，且x+y=1，
∴
+=（x+y）（+）=5++≥9，当且仅当 x=且 y=时，取等号．故“
+≥a恒成立”等价于a≤9．而{a|a≤8}?{a|a≤9}，故“a≤8”是“
+≥a恒成立”的充分不必要条件，故选A．
点评：本题主要考查充分条件、必要条件、充要条件的定义，基本不等式的应用，体现了等价转化的数学思想，
属于基础题．
练习册系列答案
相关题目
+
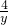≥a恒成立”的