题目内容
已知a∈R，x＞0，y＞0，且x+y=1，则“a≤8”是“
+
≥a恒成立”的（ ）
| 1 |
| x |
| 4 |
| y |
| A．充分不必要条件 | B．必要不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |
∵已知a∈R，x＞0，y＞0，且x+y=1，
∴
+
=（x+y）（
+
）=5+
+
≥9，当且仅当 x=
且 y=
时，取等号．
故“
+
≥a恒成立”等价于a≤9．
而{a|a≤8}?{a|a≤9}，故“a≤8”是“
+
≥a恒成立”的充分不必要条件，
故选A．
∴
| 1 |
| x |
| 4 |
| y |
| 1 |
| x |
| 4 |
| y |
| y |
| x |
| 4x |
| y |
| 1 |
| 3 |
| 2 |
| 3 |
故“
| 1 |
| x |
| 4 |
| y |
而{a|a≤8}?{a|a≤9}，故“a≤8”是“
| 1 |
| x |
| 4 |
| y |
故选A．
练习册系列答案
赢在课堂名师课时计划系列答案
相关题目
+
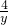≥a恒成立”的
+
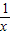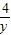≥a恒成立”的（ ）