题目内容
正四棱锥(底面为正方形,顶点在底面上的射影是底面的中心)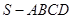 的底面边长为2,高为2,
的底面边长为2,高为2,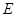 为边
为边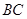 的中点,动点
的中点,动点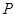 在表面上运动,并且总保持
在表面上运动,并且总保持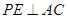 ,则动点
,则动点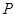 的轨迹的周长为( )
的轨迹的周长为( )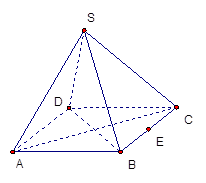
A.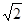 | B.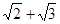 | C.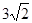 | D.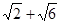 |
D
解析试题分析:取SC的中点F,CD的中点H,连接EF、EH。在正四棱锥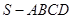 中,易知AC⊥面SDB,又面EFH//面SDB,所以AC⊥面EFH,所以动点P在线段EF、FH、EH上运动总能保持
中,易知AC⊥面SDB,又面EFH//面SDB,所以AC⊥面EFH,所以动点P在线段EF、FH、EH上运动总能保持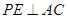 。EH=
。EH= ,所以动点
,所以动点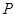 的轨迹的周长为
的轨迹的周长为 .
.
考点:正四棱锥的结构特征;线面垂直的判定定理;线面垂直的性质定理。
点评:分析出点P的轨迹是做本题的关键,注意是利用线面垂直来推线线垂直。考查了学生逻辑推理能力、分析问题和解决问题的能力。属于中档题。

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
已知m,n是两条不重合的直线, 是三个两两不重合的平面,给出下列四个命题:
是三个两两不重合的平面,给出下列四个命题:
①若m
 ,m
,m
 ,则
,则 ∥
∥ ; ②若
; ②若

 ,
,

 则
则 ∥
∥
③若m// ,n //
,n // ,m//n 则
,m//n 则 //
// ④若m
④若m
 ,m//
,m// ,则
,则


其中真命题是( )
| A.①和② | B.①和③ | C.③和④ | D.①和④ |
在空间四边形 中,
中, 分别为
分别为 的中点,若
的中点,若 则
则 与
与 所成的角为
所成的角为
A. | B. | C. | D. |
下列结论中正确的是( )
| A.平行于平面内两条直线的平面,一定平行于这个平面 |
| B.一条直线平行于一个平面内的无数条直线,则这条直线与该平面平行 |
| C.两个平面分别与第三个平面相交,若交线平行则两平面平行 |
| D.在两个平行平面中,一平面内的一条直线必平行于另一个平面 |
在三棱柱 中,各棱长相等,侧掕垂直于底面,点
中,各棱长相等,侧掕垂直于底面,点 是侧面
是侧面 的中心,则
的中心,则 与平面
与平面 所成角的大小是 ( )
所成角的大小是 ( )
A.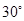 | B.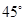 | C. | D. |
设 、b是两条不同的直线,
、b是两条不同的直线, 、
、 是两个不同的平面,则下列四个命题中正确的是( )
是两个不同的平面,则下列四个命题中正确的是( )
A.若 ⊥b, ⊥b, ⊥ ⊥ ,则b∥ ,则b∥ | B.若 ∥ ∥ , , ⊥ ⊥ ,则 ,则 ⊥ ⊥ |
C.若 ⊥ ⊥ , , ⊥ ⊥ ,则 ,则  ∥ ∥ | D.若 ⊥b, ⊥b, ⊥ ⊥ ,b⊥ ,b⊥ ,则 ,则 ⊥ ⊥ |
在正三棱锥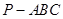 中,
中,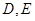 分别是
分别是 的中点,有下列三个论断:
的中点,有下列三个论断:
①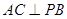 ;②
;②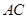 //平面
//平面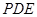 ;③
;③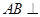 平面
平面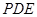 ,
,
其中正确论断的个数为 ( )
| A.3个 | B.2个 | C.1个 | D.0个 |



 =
= =
= ,则( )
,则( )