题目内容
19.已知函数f(x)=sin2x-2$\sqrt{2}$asin(x+$\frac{π}{4}$)+2,设t=sinx+cosx,且x∈(-$\frac{π}{4}$,$\frac{3π}{4}$)(1)试将函数f(x)表示成关于t的函数g(t),并写出t的范围;
(2)若g(t)≥0恒成立,求实数a的取值范围;
(3)若方程f(x)=0有四个不同的实数根,求a的取值范围.
分析 (1)利用三角函数恒等变换可得t=$\sqrt{2}$sin(x+$\frac{π}{4}$),且x∈(-$\frac{π}{4}$,$\frac{3π}{4}$),t∈(0,$\sqrt{2}$],
可求g(t)=t2-2at+1,t∈(0,$\sqrt{2}$].
(2)由题意可得a≤$\frac{{t}^{2}+1}{2t}=\frac{t}{2}+\frac{1}{2t}$,在t∈(0,$\sqrt{2}$]上恒成立,令H(t)=$\frac{t}{2}+\frac{1}{2t}$,可求H′(t)=$\frac{1}{2}-\frac{1}{2{t}^{2}}$,由$\left\{\begin{array}{l}{H′(t)≥0}\\{0<t≤\sqrt{2}}\end{array}\right.$,$\left\{\begin{array}{l}{H′(t)<0}\\{0<t≤\sqrt{2}}\end{array}\right.$,即可利用函数的单调性解得a的取值范围.
(3)方程f(x)=0有四个不同的解等价于g(t)在(0,$\sqrt{2}$)上有两个不相等的实根,问题转化为g(t)=t2-2at+1在(0,$\sqrt{2}$]上有两个不相等的实根的条件为:$\left\{\begin{array}{l}{\stackrel{△=4{a}^{2}-4>0}{-\frac{-2a}{2}=a∈(0,\sqrt{2})}}\\{\stackrel{g(0)>0}{g(\sqrt{2})>0}}\end{array}\right.$,从而解得a的范围.
解答 解:(1)∵t=sinx+cosx=$\sqrt{2}$sin(x+$\frac{π}{4}$),且x∈(-$\frac{π}{4}$,$\frac{3π}{4}$),
∴x+$\frac{π}{4}$∈(0,π),
∴t=$\sqrt{2}$sin(x+$\frac{π}{4}$)∈(0,$\sqrt{2}$],
∴sin2x=2sinxcosx=(sinx+cosx)2-(sin2x+cos2x)=t2-1,
∴g(t)=sin2x-2$\sqrt{2}$asin(x+$\frac{π}{4}$)+2
=t2-1-2at+2
=t2-2at+1,t∈(0,$\sqrt{2}$].
(2)∵g(t)=t2-2at+1≥0恒成立,t∈(0,$\sqrt{2}$],
∴a≤$\frac{{t}^{2}+1}{2t}=\frac{t}{2}+\frac{1}{2t}$,在t∈(0,$\sqrt{2}$]上恒成立.
令H(t)=$\frac{t}{2}+\frac{1}{2t}$,则H′(t)=$\frac{1}{2}-\frac{1}{2{t}^{2}}$,由$\left\{\begin{array}{l}{H′(t)≥0}\\{0<t≤\sqrt{2}}\end{array}\right.$,$\left\{\begin{array}{l}{H′(t)<0}\\{0<t≤\sqrt{2}}\end{array}\right.$,
可得H(t)在(0,1]单调递减,在[1,$\sqrt{2}$]上单调递增,
所以H(t)min=H(1)=1,
所以:a≤H(t)min=H(1)=1时,在t∈(0,$\sqrt{2}$]上g(t)≥0恒成立.
(3)方程f(x)=0有四个不同的解等价于g(t)在(0,$\sqrt{2}$)上有两个不相等的实根,
问题转化为g(t)=t2-2at+1在(0,$\sqrt{2}$]上有两个不相等的实根的条件为:$\left\{\begin{array}{l}{\stackrel{△=4{a}^{2}-4>0}{-\frac{-2a}{2}=a∈(0,\sqrt{2})}}\\{\stackrel{g(0)>0}{g(\sqrt{2})>0}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{\stackrel{a>1或a<-1}{0<a<\sqrt{2}}}\\{\stackrel{1>0}{a<\frac{3\sqrt{2}}{4}}}\end{array}\right.$,可得:1<a<$\frac{3\sqrt{2}}{4}$.
故若方程f(x)=0有四个不同的实数根,a∈(1,$\frac{3\sqrt{2}}{4}$).
点评 本题主要考查了三角函数恒等变换的应用,考查了导数的概念及应用,根的存在性及根的个数判断,综合性强,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | {2} | B. | {1} | C. | [-2,0] | D. | {-2,-1,0} |
| A. | a>3 | B. | a>0且a≠1 | C. | a<3 | D. | 2<a<3 |
| A. | 递增数列 | B. | 递减数列 | C. | 摆动数列 | D. | 常数列 |
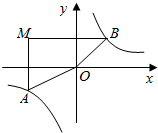 如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数$y=\frac{4}{x}$的图象交于A、B两点,则四边形MAOB的面积为10.
如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数$y=\frac{4}{x}$的图象交于A、B两点,则四边形MAOB的面积为10.