题目内容
(文科)(本小题满分12分)长方体 中,
中,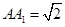 ,
, ,
, 是底面对角线的交点.
是底面对角线的交点.
(Ⅰ) 求证: 平面
平面 ;
;
(Ⅱ) 求证: 平面
平面 ;
;
(Ⅲ) 求三棱锥 的体积。
的体积。
(Ⅰ)由 ,
,
且 在平面
在平面 外.得
外.得 平面;
平面;
(Ⅱ)连结 得到
得到 平面
平面 ;
;
又∵ 在
在 上,可得
上,可得 ;
;
计算 ;
;
同理: ∵
∵ 中,
中,
推出 平面
平面 。
。
(Ⅲ)
 。
。
解析试题分析:(Ⅰ) 证明:依题意: ,
,
且 在平面
在平面 外.…2分
外.…2分
∴ 平面
平面 3分
3分
(Ⅱ) 证明:连结 ∵
∵

∴ 平面
平面 4分
4分
又∵ 在
在 上,∴
上,∴ 在平面
在平面 上
上
∴ 5分
5分
∵ ∴
∴
∴ ∴
∴ 中,
中, 6分
6分
同理: ∵
∵ 中,
中,
∴ 7分,∴
7分,∴ 平面
平面 8分
8分
(Ⅲ)解:∵ 平面
平面 ∴所求体积
∴所求体积
 12分
12分
考点:本题主要考查立体几何中的平行关系、垂直关系,几何体体积的计算。
点评:典型题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤。利用向量可简化证明过程。本题难度不大。

练习册系列答案
相关题目
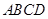 中,
中,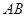 ,
,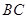 ,
,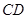 两两互相垂直,且
两两互相垂直,且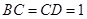 .
.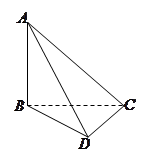
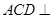 平面
平面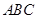 ;
;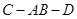 的大小;
的大小; 与平面
与平面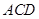 所成的角为
所成的角为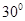 ,求线段
,求线段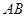 为圆
为圆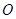 的直径,点
的直径,点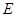 、
、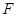 在圆
在圆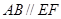 ,矩形
,矩形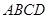 所在的平面与圆
所在的平面与圆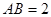 ,
,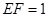 .
.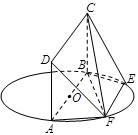
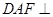 平面
平面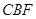 ;
;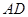 的长为何值时,平面
的长为何值时,平面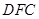 与平面
与平面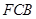 所成的锐二面角的大小为
所成的锐二面角的大小为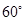 ?
?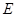 是以
是以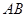 为直径的半圆上异于
为直径的半圆上异于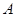 、
、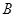 的点,矩形
的点,矩形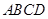 所在的平面垂直于该半圆所在的平面,且
所在的平面垂直于该半圆所在的平面,且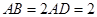 .
.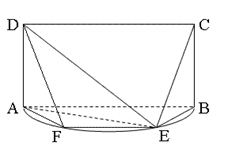
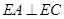 ;
;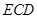 与半圆弧的另一个交点为
与半圆弧的另一个交点为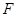 .
.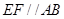 ;
;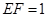 ,求三棱锥
,求三棱锥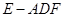 的体积.
的体积. 的底面
的底面 为菱 形 ,AC∩BD=O侧棱
为菱 形 ,AC∩BD=O侧棱 ⊥BD,点F为
⊥BD,点F为 的中点.
的中点.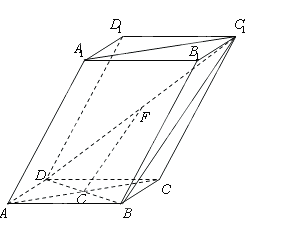
 平面
平面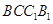 ;
;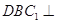 平面
平面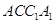 .
. 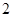 的正方体
的正方体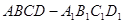 中,
中,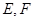 分别为
分别为 的中点.
的中点.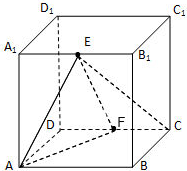
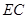 与平面
与平面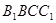 所 成 角的大小;
所 成 角的大小;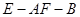 的大小.
的大小. 中.
中.
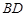 与
与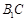 所成的角;
所成的角;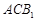
 平面
平面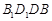 .
. 中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点.
中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点.
 中,
中, ,
, ,
, ,
, 分别是
分别是 的中点.
的中点.
 ;
; ;
; ,求二面角
,求二面角 的大小.
的大小.