题目内容
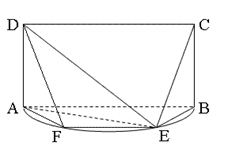
如图,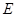 是以
是以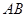 为直径的半圆上异于
为直径的半圆上异于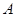 、
、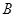 的点,矩形
的点,矩形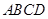 所在的平面垂直于该半圆所在的平面,且
所在的平面垂直于该半圆所在的平面,且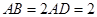 .
.
(Ⅰ)求证: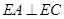 ;
;
(Ⅱ)设平面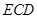 与半圆弧的另一个交点为
与半圆弧的另一个交点为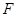 .
.
①试证: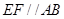 ;
;
②若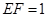 ,求三棱锥
,求三棱锥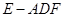 的体积.
的体积.
(Ⅰ)先证 面
面 (Ⅱ)①先证
(Ⅱ)①先证 平面
平面 ②
② .
.
解析试题分析:(Ⅰ)∵平面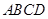
 平面
平面 ,
,
面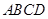
 面
面
 ,
, ,
, 面
面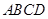 ,
,
∴ 面
面 .
.
又∵ 面
面 ,∴
,∴ .
.
∵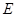 在以
在以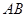 为直径的半圆上,∴
为直径的半圆上,∴ ,
,
又∵ ,
, 面
面 ,∴
,∴ 面
面 .
.
又∵ 面
面 ,∴
,∴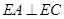 .
.
(Ⅱ)① ∵ ,
, 面
面 ,
, 面
面 ,
,
∴ 平面
平面 .
.
又∵ 面
面 ,平面
,平面 平面
平面
 ,
,
∴ .
.
②取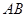 中点
中点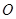 ,
, 的中点
的中点 ,
,
在 中,
中, ,
, ,∴
,∴ .
.
(Ⅰ)已证得 面
面 ,又已知
,又已知 ,
,
∴ 平面
平面 .
.
故
 .
.
考点:直线与平面平行的判定;棱柱、棱锥、棱台的体积;直线与平面垂直的判定.
点评:本题主要考查线面垂直与线面平行的证明以及三棱锥体积的计算.是对立体几何知识的综合考查,难度不大,属于中档题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
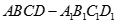 ,
, 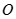 是底
是底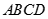 对角线的交点.
对角线的交点.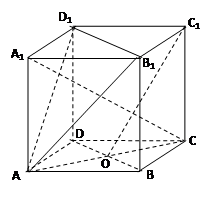
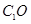 ∥面
∥面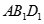 ;
;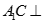 面
面
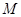 ,
, 分别是
分别是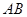 ,
, 的中点.
的中点.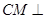 平面
平面 ;
;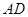 上(含
上(含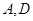 端点)确定一点
端点)确定一点 ,使得
,使得 ∥平面
∥平面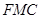 ,并给出证明.
,并给出证明.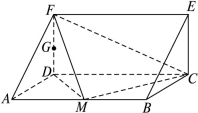
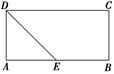
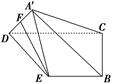
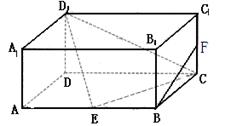
 中,
中,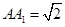 ,
, ,
, 是底面对角线的交点.
是底面对角线的交点.
 平面
平面 ;
; 平面
平面 的体积。
的体积。

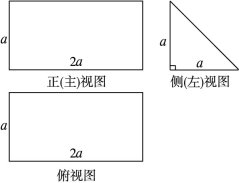
 平面ABCD,EF∥AB, AB=2EF=2AD=4,
平面ABCD,EF∥AB, AB=2EF=2AD=4, .
.