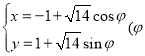题目内容
【题目】已知![]() ,函数
,函数![]() ,其中e=2.71828…为自然对数的底数.
,其中e=2.71828…为自然对数的底数.
(Ⅰ)证明:函数![]() 在
在![]() 上有唯一零点;
上有唯一零点;
(Ⅱ)记x0为函数![]() 在
在![]() 上的零点,证明:
上的零点,证明:
(ⅰ)![]() ;
;
(ⅱ)![]() .
.
【答案】(I)证明见解析,(II)(i)证明见解析,(ii)证明见解析.
【解析】
(I)先利用导数研究函数单调性,再结合零点存在定理证明结论;
(II)(i)先根据零点化简不等式,转化求两个不等式恒成立,构造差函数,利用导数求其单调性,根据单调性确定最值,即可证得不等式;
(ii)先根据零点条件转化:![]() ,再根据
,再根据![]() 放缩,转化为证明不等式
放缩,转化为证明不等式![]() ,最后构造差函数,利用导数进行证明.
,最后构造差函数,利用导数进行证明.
(I)![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,
,
所以由零点存在定理得![]() 在
在![]() 上有唯一零点;
上有唯一零点;
(II)(i)![]() ,
,
![]() ,
,
令![]()
一方面:![]()
![]() ,
,
![]() 在
在![]() 单调递增,
单调递增,![]() ,
,
![]() ,
,
另一方面:![]() ,
,
所以当![]() 时,
时,![]() 成立,
成立,
因此只需证明当![]() 时
时![]() ,
,
因为![]()
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() ,
,
![]() 在
在![]() 单调递减,
单调递减,![]() ,
,![]() ,
,
综上,![]() .
.
(ii)![]() ,
,
![]() ,
,![]() ,
,
![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
![]() ,
,
只需证明![]() ,
,
即只需证明![]() ,
,
令![]() ,
,
则![]() ,
,
![]() ,即
,即![]() 成立,
成立,
因此![]() .
.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目