题目内容
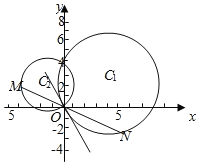
【题目】已知以点![]() 为圆心的圆过点
为圆心的圆过点![]() 和
和![]() ,线段
,线段![]() 的垂直平分线交圆
的垂直平分线交圆![]() 于点
于点![]() 、
、![]() ,且
,且![]() ,
,
(1)求直线![]() 的方程; (2)求圆
的方程; (2)求圆![]() 的方程。
的方程。
(3)设点![]() 在圆
在圆![]() 上,试探究使
上,试探究使![]() 的面积为 8 的点
的面积为 8 的点![]() 共有几个?证明你的结论
共有几个?证明你的结论
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)2
;(3)2
【解析】分析:(1)根据直线![]() 是线段
是线段![]() 的垂直平分线的方程,求出线段
的垂直平分线的方程,求出线段![]() 中点坐标和直线
中点坐标和直线![]() 的斜率,即可解直线
的斜率,即可解直线![]() 的方程;
的方程;
(2)设圆心![]() ,则由
,则由![]() 在
在![]() 上得
上得![]() ,又直径
,又直径![]() ,得
,得![]() ,求得
,求得![]() 或
或![]() ,分别代入,即可求解圆的方程;
,分别代入,即可求解圆的方程;
(3)由![]() ,由三角形的面积公式,得点
,由三角形的面积公式,得点![]() 到直线
到直线![]() 的距离,再由圆心到直线
的距离,再由圆心到直线![]() 的距离得圆
的距离得圆![]() 的半径,进而得到面积结论.
的半径,进而得到面积结论.
详解:(1)∵![]() ,
,![]() 的中点坐标为
的中点坐标为![]()
∴直线![]() 的方程为:
的方程为:![]() 即
即![]()
(2)设圆心![]() ,则由
,则由![]() 在
在![]() 上得
上得![]() ①
①
又直径![]() ,∴
,∴![]() ∴
∴![]() ②
②
①代入②消去![]() 得
得![]() ,解得
,解得![]() 或
或![]()
当![]() 时
时![]() ,当
,当![]() 时
时![]() ∴圆心
∴圆心![]() 或
或![]()
∴圆![]() 的方程为:
的方程为:![]() 或
或![]()
(3)∵![]()
∴当![]() 面积为 8 时,点
面积为 8 时,点![]() 到直线
到直线![]() 的距离为
的距离为![]()
又圆心到直线![]() 的距离为
的距离为![]() ,圆
,圆![]() 的半径
的半径![]() ,且
,且![]()
∴圆上共有两个点![]() ,使
,使![]() 的面积为 8
的面积为 8

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目