题目内容
已知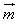 =(2cosx+2
=(2cosx+2 sinx,1),
sinx,1),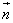 =(cosx,-y),满足
=(cosx,-y),满足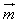 ·
· =0,
=0,
(Ⅰ)将y表示为x的函数f(x),并求f(x)的最小正周期;
(Ⅱ)已知a,b,c分别为△ABC的三个内角A,B,C对应的边长,若f(x)≤ 对所有x∈R恒成立,且a=2,求b+c的取值范围。
对所有x∈R恒成立,且a=2,求b+c的取值范围。
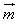 =(2cosx+2
=(2cosx+2 sinx,1),
sinx,1),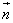 =(cosx,-y),满足
=(cosx,-y),满足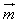 ·
· =0,
=0,(Ⅰ)将y表示为x的函数f(x),并求f(x)的最小正周期;
(Ⅱ)已知a,b,c分别为△ABC的三个内角A,B,C对应的边长,若f(x)≤
 对所有x∈R恒成立,且a=2,求b+c的取值范围。
对所有x∈R恒成立,且a=2,求b+c的取值范围。 解:(Ⅰ)由 ,
,
即 ,
,
所以 ,其最小正周期为π。
,其最小正周期为π。
(Ⅱ)因为 对所有x∈R恒成立,
对所有x∈R恒成立,
所以 ,
,
因为A为三角形内角,
所以 ,
,
由正弦定理得 ,
,
 ,
,
 ,
,
∴ ,
,
∴b+c∈ ,
,
所以b+c的取值范围为 。
。
 ,
,即
 ,
,所以
 ,其最小正周期为π。
,其最小正周期为π。(Ⅱ)因为
 对所有x∈R恒成立,
对所有x∈R恒成立,所以
 ,
,因为A为三角形内角,
所以
 ,
,由正弦定理得
 ,
, ,
, ,
,∴
 ,
,∴b+c∈
 ,
,所以b+c的取值范围为
 。
。 
练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目