题目内容
圆C:(x-1)2+(y-1)2=1关于直线y=5x-4对称的圆的方程为 .
考点:直线与圆的位置关系
专题:直线与圆
分析:先根据圆C的方程求出圆心和半径,再根据垂直及中点在轴上这两个条件,求出圆心关于直线的对称点的坐标,即可求得关于直线对称的圆的方程.
解答:
解:设圆心C(1,1)关于直线y=5x-4对称的点的坐标为C′(a,b),
则由
,求得
,故C′(1,1),故对称圆的方程为(x-1)2+(y-1)2=1,
故答案为:(x-1)2+(y-1)2=1.
则由
|
|
故答案为:(x-1)2+(y-1)2=1.
点评:本题主要考查求一个圆关于一条直线的对称的圆的方程的方法,关键是求出对称圆的圆心坐标,属于基础题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
在正方体ABCD-A1B1C1D1中,与棱AA1垂直的棱共有( )条.
| A、2 | B、4 | C、6 | D、8 |
如图所示的工序流程图中,设备采购的下一道工序是( )


| A、设备安装 | B、土建设计 |
| C、厂房土建 | D、工程设计 |
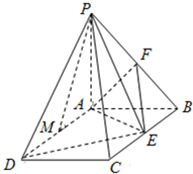 如图,已知PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,AD=
如图,已知PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,AD=