题目内容
19．已知等差数列{an}的首项为1，公差为2，则数列$\{\frac{1}{{{a_n}{a_{n+1}}}}\}$的前n项和Sn=$\frac{n}{2n+1}$．分析 由an=2n-1．可得$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{（2n-1）（2n+1）}$=$\frac{1}{2}（\frac{1}{2n-1}-\frac{1}{2n+1}）$．利用“裂项求和”方法即可得出．
解答 解：∵an=1+2（n-1）=2n-1．
∴$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{（2n-1）（2n+1）}$=$\frac{1}{2}（\frac{1}{2n-1}-\frac{1}{2n+1}）$．
数列$\{\frac{1}{{{a_n}{a_{n+1}}}}\}$的前n项和Sn=$\frac{1}{2}[（1-\frac{1}{3}）+（\frac{1}{3}-\frac{1}{5}）$+…+$（\frac{1}{2n-1}-\frac{1}{2n+1}）]$
=$\frac{1}{2}（1-\frac{1}{2n+1}）$
=$\frac{n}{2n+1}$．
故答案为：$\frac{n}{2n+1}$．
点评 本题考查了等差数列的通项公式、“裂项求和”方法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
9．已知圆（x-1）2+y2=4内一点P（2，1），则过P点的直径所在的直线方程是（ ）
| A． | x-y-1=0 | B． | x+y-3=0 | C． | x+y+3=0 | D． | x=2 |
7．函数$f（x）=\frac{{{e^x}-{e^{-x}}}}{2}，x∈R$，当$0≤θ≤\frac{π}{2}$时，f（msinθ）+f（1-m）＞0恒成立，则实数m的取值范围是（-∞，1]．
14．已知实数x，y满足$\left\{{\begin{array}{l}{x+y≥4}\\{x-y≤2}\\{3y-x≤4}\end{array}}\right.$，则$\frac{y}{x}$的最小值为（ ）
| A． | 1 | B． | $\frac{1}{3}$ | C． | $\frac{3}{5}$ | D． | $\frac{1}{4}$ |
4．命题p：?x＜0，2x＞x，命题q：?x∈R，x2+x+1＜0，则下列命题正确的是（ ）
| A． | （￢p）∨q为真 | B． | p∨q为真 | C． | p∧（￢q）为假 | D． | （￢p）∧（￢q）为真 |
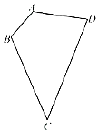如图所示，已知平面四边形ABCD为凸四边形（凸四边形即任取平面四边形一边所在直线，其余各边均在此直线的同侧），且AB=1，BC=3，CD=4，DA=2，则平面四边形ABCD面积的最大值为$2\sqrt{6}$．
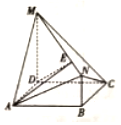如图，四边形ABCD是矩形，MD⊥平面ABCD，NB∥MD，且AD=2，NB=1，CD=MD=3．