题目内容
三棱锥P-ABC中,PA⊥底面ABC,PA=3,底面ABC是边长为2的正三角形,则三棱锥P-ABC的表面积等于 .
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:根据三棱锥的条件,求出△PBC的高,即可求出三棱锥的表面积.
解答:
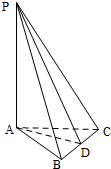 解:取BC的中点D,连结AD,PD,
解:取BC的中点D,连结AD,PD,
∵PA⊥底面ABC,PA=3,底面ABC是边长为2的正三角形,
∴PB=PC=
=
=
,BD=1,
则PD=
=
=
=2
,
则三角形PAB的面积S=
×3×2=3,三角形PAC的面积S=
×3×2=3,
三角形ABC的面积S=
×2×2×
=
,三角形PBC的面积S=
×2×2
=2
,
则三棱锥P-ABC的表面积等于3+3+
+2
=6+3
,
故答案为:6+3
 解:取BC的中点D,连结AD,PD,
解:取BC的中点D,连结AD,PD,∵PA⊥底面ABC,PA=3,底面ABC是边长为2的正三角形,
∴PB=PC=
| PA2+AB2 |
| 9+4 |
| 13 |
则PD=
| PB2-BD2 |
| 13-1 |
| 12 |
| 3 |
则三角形PAB的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
三角形ABC的面积S=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
则三棱锥P-ABC的表面积等于3+3+
| 3 |
| 3 |
| 3 |
故答案为:6+3
| 3 |
点评:本题主要考查三棱锥的表面积的计算,根据三角形的面积公式是解决本题的关键.

练习册系列答案
相关题目
点P在双曲线
-
=1(a>0,b>0)上,F1,F2分别是双曲线的左、右焦点∠F1PF2=90°,且△F1PF2的三条边长之比为3:4:5.则双曲线的渐近线方程是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、y=±2
| ||
| B、y=±4x | ||
C、y=±2
| ||
D、y=±2
|