题目内容
3. 如图,在直四棱柱ABCD-A1B1C1D1中,∠BAD=60°,AB=BD,BC=CD.
如图,在直四棱柱ABCD-A1B1C1D1中,∠BAD=60°,AB=BD,BC=CD.(1)求证:平面ACC1A1⊥平面A1BD;
(2)AB=AA1=2,求三棱锥B1-A1BD的体积.
分析 (1)由△ABD为等边三角形可得AB=AD,故△ABC≌△ADC,得出AC平分∠BAD,故AC⊥BD,由A1A⊥平面ABCD得A1A⊥BD,故BD⊥平面ACC1A1,于是平面ACC1A1⊥平面A1BD;
(2)取AB的中点M,连结DM,则可证DM⊥平面ABB1A1,故而V${\;}_{{B}_{1}-{A}_{1}BD}$=V${\;}_{D-{A}_{1}{B}_{1}B}$=$\frac{1}{3}{S}_{△{A}_{1}{B}_{1}B}•DM$.
解答 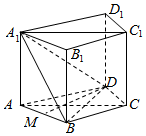 证明:(1)∵AB=BD,∠BAD=60°,
证明:(1)∵AB=BD,∠BAD=60°,
∴△ABD是等边三角形
∴AB=AD,又BC=CD,AC为公共边,
∴△ABC≌△ADC,
∴∠BAC=∠DAC,即AC为∠BAD的平分线,
∴AC⊥BD.
∵A1A⊥平面ABCD,BD?平面ABCD,
∴A1A⊥BD,又A1A?平面ACC1A1,AC?平面ACC1A1,A1A∩AC=A,
∴BD⊥平面ACC1A1,∵BD?平面A1BD,
∴平面ACC1A1⊥平面A1BD.
(2)取AB的中点M,连结DM,
∵△ABD是等边三角形,AB=2,∴DM⊥AB,DM=$\sqrt{3}$.
∵A1A⊥平面ABCD,DM?平面ABCD,
∴A1A⊥DM,又A1A?平面ABB1A1,AB?平面ABB1A1,A1A∩AB=A,
∴DM⊥平面ABB1A1,
∴V${\;}_{{B}_{1}-{A}_{1}BD}$=V${\;}_{D-{A}_{1}{B}_{1}B}$=$\frac{1}{3}{S}_{△{A}_{1}{B}_{1}B}•DM$=$\frac{1}{3}×\frac{1}{2}×2×2×\sqrt{3}=\frac{2\sqrt{3}}{3}$.
点评 本题考查了线面垂直,面面垂直的判定,棱锥的体积计算,属于中档题.

 科学实验活动册系列答案
科学实验活动册系列答案| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{3}$+1 |
| A. | $\frac{\sqrt{5}}{2}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\sqrt{6}$ |
| A. | (-∞,0) | B. | (-∞,0] | C. | (-∞,3) | D. | (-∞,3] |
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
| A. | $\frac{\sqrt{3}+2}{2}$ | B. | $\sqrt{3}$+2 | C. | $\frac{\sqrt{3}+\sqrt{6}}{2}$ | D. | $\sqrt{3}$+$\sqrt{6}$ |