Question

如图：设一正方形纸片ABCD边长为m，从此纸片中裁剪出一个正方形和四个全等的等腰三角形，恰好能做成一个正四棱锥（粘接损耗不计），图中AH⊥PQ，O为正四棱锥底的中心
（1）若正四棱锥的棱长都相等，求这个正四棱锥的体积V；
（2）设等腰三角形底角为x，试把正四棱锥侧面积S表示为x的函数，并求S的范围．

Answer 1

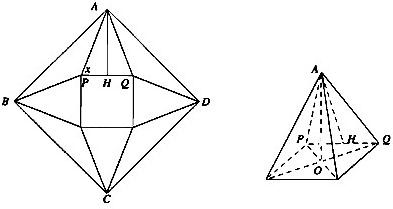
分析：（1）先设正四棱锥底面边长为y，由条件知为△APQ等边三角形，又AH⊥PQ，AH=

3

2

y，∴OA=

AH2-OH2

=

2

2

y，再由2AH+y=AC得y=

2 m

3 +1

∴根据体积公式求解．
（2）按照（1）的思路：则有AH=

y

2

tanx由2AH+y=AC得y=

2 m

tanx+1

，再由侧面积公式建立模型．用导数研究最值．

解答：解：（1）设正四棱锥底面边长为y，由条件知为△APQ等边三角形，又AH⊥PQ，
∴AH=

3

2

y，
∵OH=

y

2

∴OA=

AH2-OH2

=

2

2

y
由2AH+y=AC得y=

2 m

3 +1

∴V=

1

3

y2•OA=

2m3

3( 3 +1)3

（2）设正四棱锥的底面边长为y
则AH=

y

2

tanx由2AH+y=AC得y=

2 m

tanx+1

，
∴S=

1

2

•4y•AH=

2m2tanx

(1+tanx)2

即为所求表达式，
∵

π

4

＜x ＜

π

2

∴tanx＞1
令t=tanx则S=

2m2t

(1+t)2

由S′= 2m2

-t2+1

(1+t)4

＜0，t∈(1，+∞)恒成立知
函数在（1，+∞）上为减函数．
∴0＜s＜

m2

2

即为所求的范围．

点评：本题主要考查通过空间几何体的结构特征，来考查如何寻求各边之间量的关系及求几何体的体积和表面积问题．