Question

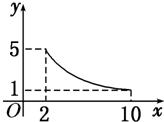
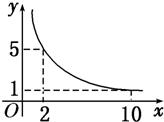
一张正方形的纸片，剪去两个一样的小矩形得到一个“E”图案，如图所示，设小矩形的长、宽分别为x，y，剪去部分的面积为20，若2≤x≤10，记y=f（x），则y=f（x）的图象是

①

（填序号）．

Answer 1

分析：由已知条件求出y=f（x），根据其定义域及最值即可得到答案．

解答：解：由题意知，2xy=20，所以y=

10

x

，则y=f（x）=

10

x

，（2≤x≤10）．
因为函数y=f（x）的定义域为[2，10]，且f（x）_min=f（10）=1，f（x）_max=f（2）=5，
故答案为：①．

点评：本题考查了函数的图象及根据实际问题求函数解析式，要充分研究函数的性质并据此作出正确判断．