题目内容
1．已知函数f（x）=x-1-lnx．（1）求函数f（x）的极值；
（2）对?x＞0，f（x）≥bx-2恒成立，求实数b的取值范围．
分析 （1）令导数大于0解出增区间，令导数小于0，解出函数的减区间，然后由极值判断规则确定出极值即可．
（2）由于f（x）≥bx-2恒成立，得到b≤1+$\frac{1}{x}$-$\frac{lnx}{x}$在（0，+∞）上恒成立，构造函数g（x）=1+$\frac{1}{x}$-$\frac{lnx}{x}$，b≤g（x）min即可
解答 解：（1）f′（x）=1-$\frac{1}{x}$，
令f′（x）＞0，得x＞1，
列表：
| x | （0，1） | 1 | （1，+∞） |
| f′（x） | - | 0 | + |
| f（x） | ↘ | 0 | ↗ |
（2）依题意对?x∈（0，+∞），f（x）≥bx-2恒成立
等价于x-1-lnx≥bx-2在（0，+∞）上恒成立
可得b≤1+$\frac{1}{x}$-$\frac{lnx}{x}$在（0，+∞）上恒成立，
令g（x）=1+$\frac{1}{x}$-$\frac{lnx}{x}$，g′（x）=$\frac{lnx-2}{{x}^{2}}$，
令g′（x）=0，得x=e2
列表：
| x | （0，e2） | e2 | （e2，+∞） |
| g'（x） | - | 0 | + |
| g（x） | ↘ | 1-$\frac{1}{{e}^{2}}$ | ↗ |
故b≤1-$\frac{1}{{e}^{2}}$．
点评 本题考查利用导数研究函数的极值，考查恒成立问题，着重考查分类讨论思想与构造函数思想的应用，体现综合分析问题与解决问题能力，属于中档题．
练习册系列答案
相关题目
11．已知向量$\overrightarrow{a}$=（2，x），$\overrightarrow{b}$=（-1，2），且$\overrightarrow{a}$⊥$\overrightarrow{b}$，则x的值是（ ）
| A． | 1 | B． | 2 | C． | $\frac{1}{4}$ | D． | $\frac{1}{2}$ |
12．己知等差数列{an}的公差d≠0，且a1，a3，a13成等比数列，若a1=1，Sn为数列{an}的前n项和，则$\frac{2{S}_{n}+144}{{a}_{n}+5}$的最小值为（ ）
| A． | 4$\sqrt{19}$-4 | B． | $\frac{27}{2}$ | C． | $\frac{121}{9}$ | D． | $\frac{67}{5}$ |
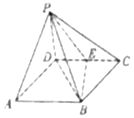如图，在四棱锥P-ABCD中，底面ABCD为菱形，且∠DAB=$\frac{π}{3}$，PA=PD，点E为CD边的中点，BD⊥PE．