设函数f．+f≥6,＜$\frac{1}{2}$的解集为非空集.求a的取值范围．题目和参考答案——青夏教育精英家教网—

题目内容

11．设函数f（x）=|x-a|+|2x-a|（a＜0）．
（1）证明：f（x）+f（-$\frac{1}{x}$）≥6；
（2）若不等式f（x）＜$\frac{1}{2}$的解集为非空集，求a的取值范围．

分析（1）根据绝对值的性质证明即可；
（2）求出f（x）的解析式，画出图象，求出a的范围即可．

解答解：（1）f（x）+f（-$\frac{1}{x}$）=（|x-a|+|2x-a|）+（|-$\frac{1}{x}$-a|+|-$\frac{2}{x}$-a|）
=（|x-a|+|-$\frac{1}{x}$-a|）+（|2x-a|+|-$\frac{2}{x}$-a|）≥|（x-a）-（-$\frac{1}{x}$-a）|+|（2x-a）-（-$\frac{2}{x}$-a）|
=|x+$\frac{1}{x}$|+|2x+$\frac{2}{x}$|=|x|+$\frac{1}{|x|}$+|2x|+$\frac{2}{|x|}$≥6（当且仅当x=±1时取等号）
（2）函数f（x）=（x-a）+（2x-a）=$\left\{\begin{array}{l}{2a-3，（x≤a）}\\{-x，（a＜x≤\frac{a}{2}}\\{3x-2a，（x＞\frac{2}{a}）}\end{array}\right.$，
图象如图所示：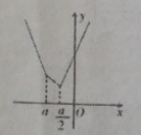

当x=$\frac{a}{2}$时，y_min=-$\frac{a}{2}$，依题意：-$\frac{a}{2}$＜$\frac{1}{2}$，解得：a＞-1，
∴a的取值范围是（-1，0）．

点评本题考查了绝对值不等式的性质，考查函数最值问题，是一道中档题．

练习册系列答案

千里马走向假期期末仿真试卷寒假系列答案

新锐图书假期园地暑假作业中原农民出版社系列答案

暑假百分百期末暑假衔接总复习系列答案

假期学习乐园暑假系列答案

暑假作业中国地图出版社系列答案

2．

如图，在矩形ABCD中，M是BC的中点，N是CD的中点，若$\overrightarrow{AC}$=λ$\overrightarrow{AM}$+μ$\overrightarrow{BN}$，则λ+μ=（　　）

19．已知函数$f（x）=lnx-\frac{1}{2}a{x}^{2}+x，a∈R$．
（1）当a=0时，求函数f（x）在（1，f（1））处的切线方程；
（2）令g（x）=f（x）-（ax-1），求函数g（x）的极值；
（3）若a=-2，正实数x₁，x₂满足f（x₁）+f（x₂）+x₁x₂=0，证明：${x}_{1}+{x}_{2}≥\frac{\sqrt{5}-1}{2}$．

6．在公比为2的等比数列{a_n}中，a₂与a₅的等差中项是$9\sqrt{3}$．
（1）求a₁的值；
（2）若函数$y=|{a_1}|sin（\frac{π}{4}x+φ）（|φ|＜π）$的一部分图象如图所示，M（-1，|a₁|），N（3，-|a₁|）为图象上的两点，设∠MPN=β，其中P与坐标原点O重合，0＜β＜π，求sin（2φ-β）的值．

16．下列说法正确的是（　　）

	A．	若命题p，￢q为真命题，则命题p∧q为真命题
	B．	“若$α=\frac{π}{6}$，则$sinα=\frac{1}{2}$”的否命题是“若$α=\frac{π}{6}$，则$sinα≠\frac{1}{2}$”
	C．	命题p：“$?{x_0}∈R，x_0^2-{x_0}-5＞0$”的否定￢p：“?x∈R，x²-x-5≤0”
	D．	若f（x）是定义在R上的函数，则“f（0）=0”是“函数f（x）是奇函数”的充要条件

3．已知函数f（x）=e^x+ax，g（x）=x•e^x+a
（1）若对于任意的实数x，都有f（x）≥1，求实数a的取值范围；
（2）令F（x）=[g（x）-f（x）]，且实数a≠0，若函数F（x）存在两个极值点x₁，x₂，证明：0＜e²F（x₁）＜4且0＜e²F（x₂）＜4．

20．设定义在R上的函数f（x）满足f（2x）=2f（x）+1且，f（1）=2．
（1）求f（0），f（2），f（4）的值；
（2）若f（x）为一次函数，且g（x）=（x-m）f（x）在（3，+∞）上为增函数，求m的取值范围．

12．$f（x）=\frac{1}{2}{x^2}-ax+alnx$有两个极值点，则a的范围是（　　）

试题分类