题目内容
已知a、b是夹角为60°的两单位向量,而向量c⊥a,c⊥b,且|c|=3,x=2a-b+c,y=3b-a-c,则cos<x,y>=_____________.
-![]()
解析:cos<x,y>=![]() 其中:x·y=-2a2-3b2-c2+7a·b=-2-3-9+7×12·cos60°=-
其中:x·y=-2a2-3b2-c2+7a·b=-2-3-9+7×12·cos60°=-![]() .
.
|x|=![]() ,
,
|y|=![]() =4.
=4.
∴cos<x,y>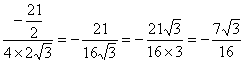 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
已知a、b是夹角为60°的两单位向量,而向量c⊥a,c⊥b,且|c|=3,x=2a-b+c,y=3b-a-c,则cos<x,y>=_____________.
-![]()
解析:cos<x,y>=![]() 其中:x·y=-2a2-3b2-c2+7a·b=-2-3-9+7×12·cos60°=-
其中:x·y=-2a2-3b2-c2+7a·b=-2-3-9+7×12·cos60°=-![]() .
.
|x|=![]() ,
,
|y|=![]() =4.
=4.
∴cos<x,y>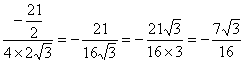 .
.

 阅读快车系列答案
阅读快车系列答案