题目内容
11．设函数f（x）=$\left\{\begin{array}{l}{\frac{1}{{x}^{2}-1}，x＜3}\\{2{x}^{-\frac{1}{2}}，x≥3}\end{array}\right.$，则f（f（$\frac{\sqrt{5}}{2}$））=1．分析 先求出$f（\frac{\sqrt{5}}{2}）$=$\frac{1}{（\frac{\sqrt{5}}{2}）^{2}-1}$=4，从而f（f（$\frac{\sqrt{5}}{2}$））=f（4），由此能求出结果．
解答 解：∵f（x）=$\left\{\begin{array}{l}{\frac{1}{{x}^{2}-1}，x＜3}\\{2{x}^{-\frac{1}{2}}，x≥3}\end{array}\right.$，
∴$f（\frac{\sqrt{5}}{2}）$=$\frac{1}{（\frac{\sqrt{5}}{2}）^{2}-1}$=4，
f（f（$\frac{\sqrt{5}}{2}$））=f（4）=$2×{4}^{-\frac{1}{2}}$=1．
故答案为：1．
点评 本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．
练习册系列答案
特高级教师点拨系列答案
相关题目
11．函数$y=\sqrt{1-x}$的定义域是（ ）
| A． | {x|0≤x≤1} | B． | {x|x≥0} | C． | {x|x≥1或x≤0} | D． | {x|x≤1} |
6．已知α、β是两个不同平面，m，n，l是三条不同直线，则下列命题正确的是（ ）
| A． | 若m∥α，n⊥β且m⊥n，则α⊥β | B． | 若m?α，n?α，l⊥n，则l⊥α | ||
| C． | 若m∥α，n⊥β且α⊥β，则m∥n | D． | 若l⊥α且l⊥β，则α∥β |
3．已知函数f（x）=$\left\{\begin{array}{l}{2^x}，（x＜2）\\ f（x-2），\;\;（x≥2）\end{array}$，则f（5）的值为（ ）
| A． | $\frac{3}{2}$ | B． | 1 | C． | 2 | D． | 3 |
如图，正方形边长是2，函数y=$\frac{1}{2x}$与正方形交于两点，向正方形内投飞镖，则飞镖落在阴影部分内的概率是$\frac{7-3ln2}{8}$．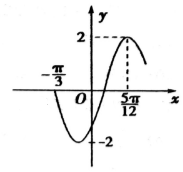
函数f（x）=Asin（ωx+φ），x∈R，（ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$）的部分图象如图所示．