题目内容
17.△ABC中,AB=3,AC=2BC,则△ABC面积的最大值为3.分析 建立如图所示的坐标系,则A(-$\frac{3}{2}$,0),B($\frac{3}{2}$,0)设C(x,y),(y≠0).根据AC=2BC,可得$\sqrt{(x+\frac{3}{2})^{2}+{y}^{2}}$=2$\sqrt{(x-\frac{3}{2})^{2}+{y}^{2}}$,化简即可得出.
解答 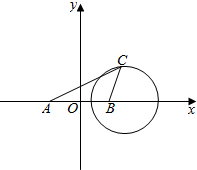 解:建立如图所示的坐标系,则A(-$\frac{3}{2}$,0),B($\frac{3}{2}$,0)设C(x,y),(y≠0)
解:建立如图所示的坐标系,则A(-$\frac{3}{2}$,0),B($\frac{3}{2}$,0)设C(x,y),(y≠0)
∵AC=2BC,
∴$\sqrt{(x+\frac{3}{2})^{2}+{y}^{2}}$=2$\sqrt{(x-\frac{3}{2})^{2}+{y}^{2}}$,
化简可得:$(x-\frac{5}{2})^{2}$+y2=4,去掉$(\frac{1}{2},0)$或$(\frac{9}{2},0)$.
即C的轨迹是以($\frac{5}{2}$,0)为圆心,2为半径的圆,
∴三角形ABC的面积的最大值为=$\frac{1}{2}×3×2$=3.
故答案为:3.
点评 本题考查了三角形面积计算公式、轨迹方程,考查了数形结合方法、推理能力与计算能力,属于中档题.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
8.“4<k<6”是“方程$\frac{x^2}{6-k}$+$\frac{y^2}{k-4}$=1表示椭圆”的( )
| A. | 既不充分也不必要条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 必要不充分条件 |
12.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)虚轴上的端点B(0,b),右焦点F,若以B为圆心的圆与C的一条渐近线相切于点P,且$\overrightarrow{BP}$$∥\overrightarrow{PF}$,则该双曲线的离心率为( )
| A. | $\sqrt{5}$ | B. | 2 | C. | $\frac{1+\sqrt{3}}{2}$ | D. | $\frac{1+\sqrt{5}}{2}$ |
6.三棱柱ABC-A1B1C1的所有棱长郡相等,∠A1AB=∠A1AC=120°,则AB1与BC1所成角的余弦值为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | 0 |