题目内容
已知2x≤256且log2x≥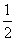 ,求函数f(x)=log2
,求函数f(x)=log2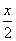 ·log
·log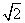
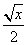 的最大值和最小值.
的最大值和最小值.
[解] 由2x≤256,得x≤8,∴log2x≤3,
即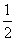 ≤log2x≤3.
≤log2x≤3.
f(x)=(log2x-1)·(log2x-2)=(log2x)2-3log2x+2
= 2-
2- .
.
当log2x= ,即x=2
,即x=2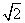 时,f(x)min=-
时,f(x)min=- ,
,
当log2x=3,即x=23=8时,f(x)max=2.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
题目内容
已知2x≤256且log2x≥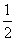 ,求函数f(x)=log2
,求函数f(x)=log2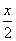 ·log
·log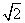
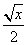 的最大值和最小值.
的最大值和最小值.
[解] 由2x≤256,得x≤8,∴log2x≤3,
即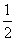 ≤log2x≤3.
≤log2x≤3.
f(x)=(log2x-1)·(log2x-2)=(log2x)2-3log2x+2
= 2-
2- .
.
当log2x= ,即x=2
,即x=2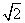 时,f(x)min=-
时,f(x)min=- ,
,
当log2x=3,即x=23=8时,f(x)max=2.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案