题目内容
如图所示，过⊙O外一点P作⊙O的切线PT，T为切点，作⊙O的割线PAB，已知PA=2，PT=4，则弦AB的长为 ．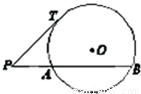
【答案】分析：过⊙O外一点P作⊙O的切线PT，作⊙O的割线PAB，由切割线定理知PT2=PA•PB，由此利用PA=2，PT=4，能求出AB的长．
解答：解：∵过⊙O外一点P作⊙O的切线PT，作⊙O的割线PAB，
∴由切割线定理知PT2=PA•PB，
∵PA=2，PT=4，
∴42=2（2+AB），
解得AB=6．
故答案为：6．
点评：本题考查与圆有关的比例线段的应用，是基础题．解题时要认真审题，仔细解答，注意切割线定理地灵活运用．
解答：解：∵过⊙O外一点P作⊙O的切线PT，作⊙O的割线PAB，
∴由切割线定理知PT2=PA•PB，
∵PA=2，PT=4，
∴42=2（2+AB），
解得AB=6．
故答案为：6．
点评：本题考查与圆有关的比例线段的应用，是基础题．解题时要认真审题，仔细解答，注意切割线定理地灵活运用．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
如图所示，过⊙O外一点P作一条直线与⊙O交于A，B两点，已知PA=2，点P到⊙O的切线长PT=4，则弦AB的长为
如图所示，过⊙O外一点A作一条直线与⊙O交于C，D两点，AB切⊙O于B，弦MN过CD的中点P．已知AC=4，AB=6，则MP•NP=
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）
（2012•香洲区模拟）（几何证明选讲选做题）如图所示，过⊙O外一点P作一条直线与⊙O交于A，B两点，己知弦AB=6，点P到⊙O的切线长PT=4，则PA=