题目内容
设f（x）=xsinx，x1、x2∈[-
，
]，且f（x1）＞f（x2），则下列结论必成立的是（ ）
| π |
| 2 |
| π |
| 2 |
分析：由题设条件，判断出f（x）是偶函数；再利用导数的性质分别判断出函数[0，
]、[-
，0]的单调性，再用等价转化思想能求出结果．
| π |
| 2 |
| π |
| 2 |
解答：解：∵f（x）=xsinx，
∴f（-x）=-xsin（-x）=xsinx=f（x），
∴函数f（x）=xsinx是偶函数，
∵f′（x）=sinx+xcosx，
∴x∈[0，
]时，f′（x）≥0，f（x）是增函数，
x∈（-
，0）时，f′（x）≤0，f（x）是减函数，
∵f（x1）＞f（x2），
∴f（|x1|）＞f（|x2|），
∴x1＞x2，
∴x12＞x22．
故选D．
∴f（-x）=-xsin（-x）=xsinx=f（x），
∴函数f（x）=xsinx是偶函数，
∵f′（x）=sinx+xcosx，
∴x∈[0，
| π |
| 2 |
x∈（-
| π |
| 2 |
∵f（x1）＞f（x2），
∴f（|x1|）＞f（|x2|），
∴x1＞x2，
∴x12＞x22．
故选D．
点评：本题考查函数的奇偶性、单调性的应用，解题时要注意导数性质的合理运用．
练习册系列答案
相关题目
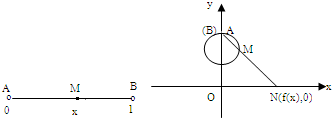设区间（0，1）内的实数x对应数轴上的点M（如图），将线段AB围成一个圆，使两端A、B恰好重合，再将这个圆放在平面直角坐标系中，使其圆心在y轴上，点A的坐标为（0，1），射线AM与ox轴交于点N（f（x），0）根据这一映射法则可得f（x）与x的函数关系式为
，又函数g（x）=|xsinπx|，则函数h（x）=f（x）﹣g（x）在
上的零点个数为（ ）